Литература(Книги)

Всё про нефть и газ \Главная \Начало \Литература \Подразделы \Книги
\Осложнения и Аварии при Бурении Нефтяных и Газовых Скважин

	Глава          ГИДРОАЭРОДИНАМИЧЕСКИЕ 1               ПРОЦЕССЫ В БУРЯЩИХСЯ СКВАЖИНАХ
	Современная технология бурения скважин предполагает систематическое использование циркулирующих промывочных агентов для транспортирования разрушенной горной породы на дневную поверхность, обеспечения необ­ходимого противодавления на проходимые скважиной гор­ные породы, подачи энергии к долоту и забойному двигате­лю, ликвидации пластовых флюидопроявлений, а также для задавливания открыто фонтанирующих скважин и т.д. Чтобы правильно выбрать технологические характеристи­ки гидравлического оборудования и определить для каждого конкретного случая необходимые параметры циркуляционно­го потока в скважине для безаварийной ее проводки или ликвидации аварии, необходимо рассмотреть основы теории и расчетные зависимости применительно к гидродинамичес­ким процессам в бурящихся скважинах. Достижения в этой области знаний базируются на реоло­гических уравнениях И. Ньютона, Ф.Ф. Шведова и Е. Бин-гама, В. Оствальда, на формулах для оценки распределения давлений в потоках флюидов, полученных Ж. Пуазейлем, Г. Стоксом, Е. Буссинеском, М.П. Воларовичем и A.M. Гут-киным, А. Фредриксоном и Р. Бердом. Существенные резуль­таты получены в результате использования теории погранич­ного слоя, разработанной Л. Прандтлем, а также расширения понятий физической сущности потоков посредством разгра­ничения режимов течения через понятие критического без­размерного комплекса, характеризующего отношение сил инерции к силам вязкостного трения, предложенное О. Рей-нольдсом, а в дальнейшем развитое Б. Хедстремом (крити­ческие числа Рейнольдса и Сен-Венана). Значительно обогащены отдельные разделы гидродинами­ки буровых процессов исследованиями гидродинамических сопротивлений в турбобурах (П.П. Шумилов), коэффициентов гидравлических сопротивлений в трубах (А.Д. Альтшуль), ме­стных сопротивлений потоку (X. Геррик).

	Важными оказались решения вопросов взаимодействия потока с взвешенными в нем твердыми частицами (Г. Стоке, Р.И. Шищенко и Б.Д. Бакланов). Гидродинамика буровых процессов как ветвь науки меха­ники сплошных сред начала формироваться в виде обобща­ющих работ Р.И. Шищенко, А.Х. Мирзаджанзаде, Н. Мако-вея. Достижения в этой области применительно к теории и практике гидродинамических процессов в бурении были сис­тематизированы в виде учебника для студентов вузов, обуча­ющихся по специальности "бурение нефтяных и газовых скважин", Е.Г. Леоновым и В.М. Исаевым (Е.Г. Леонов, В.И. Исаев. Гидроаэромеханика в бурении. — М: Недра, 1987). Сознавая, что авторами упомянутого учебника глубоко проработан материал дисциплины, а изложение его ориенти­ровано в основном на студентов, составители настоящего учебника стремились изложить материал этой главы как можно ближе к изложению аналогичных разделов учеб­ника.
	1.1. РАВНОВЕСИЕ И ДВИЖЕНИЕ ТВЕРДЫХ ЧАСТИЦ В ЖИДКОСТИ, ГАЗЕ И ГАЗОЖИДКОСТНОЙ СМЕСИ Осколки разрушенных горных пород (шлам), поступающие с забоя и стенок скважины, уносятся потоком промывочной жидкости, газа или газожидкостной смеси. Ниже рассмотрены закономерности взаимодействия потока с частицами породы на забое и в заколонном пространстве скважины, необходимые для расчетов подачи насосов при промывке, компрессоров при продувке или тех и других при бурении с использованием аэрированной жидкости. Витание твердых частиц в потоках жидкости, газа и газожидкостной смеси Рассмотрим движение твердой частицы со средней скоростью v4 в восходящем вертикальном потоке жидкости, текущей со скоростью vn. В общем случае скоро­сти потока и частицы относительно неподвижных стенок 6

	скважины разные. Обычно плотность частиц горных пород больше плотности жидкости, поэтому относительная ско­рость (рис. 1.1, а) v = v — v                                                                                  (11) voth            vn            V4*                                                                                                                                 VXt±y Принято, что частица, витая в потоке, имеет скорость v4 = 0. Тогда скорость потока в (1.1) при v4 = 0 называется скоростью витания vB: vn = vB.                                                                                  (1.2) Чтобы выбрать среднюю скорость потока, обеспечиваю­щую транспорт частиц в кольцевом канале на дневную по­верхность, нужно уметь определять скорости vB и v4. 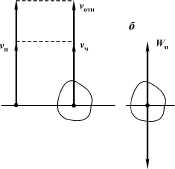Равновесие частицы в восходящем потоке обеспечивается равенством действующих на нее сил, схематично показанных на рис. 1.1, б. На частицу действует равнодействующая выталкивающей силы и силы тяжести: R = V(p4 - pjgr,                                                                   (1.3) где V — объем частицы; рч, рж — плотность соответственно частицы и жидкости; д — ускорение свободного падения. Сила R уравновешивается силой сопротивления Wn, кото­рая зависит от реологических свойств жидкости, режима об­текания, концентрации и формы частиц. В дальнейшем будем рассматривать единичную сферическую частицу с эквивалент-
	а
	Рис. 1.1. Векторы скоростей (а) и сил [б) для витающей в жидкости твердой частицы	R

	.1/3 ным диаметром d4 =f— в неограниченной среде. Экспе- I я ) риментально установлено, что в этом случае частица при об­текании имеет наименьшее сопротивление. Формула для оп­ределения силы сопротивления частицы при обтекании ее вязкой жидкостью, согласно формуле Стокса, имеет вид Wu = 3nyid4vB.                                                                             (1.4) Эта формула справедлива для чисел Рейнольдса Re = = vBd4pm/\i < 1. При любых значениях Re силу сопротивления можно вы­разить в общей форме Wn=Cwp^/S,                                                      (1.5) где Cw — коэффициент сопротивления; S — площадь наи­большего сечения частицы, перпендикулярного к потоку. Формула (1.5) переходит в (1.4) при Cw = 24/Re.                                                                          (1.6) Приравнивая (1.3) и (1.5) и подставляя V = jtc^/6 и S = ndl / 4, получаем скорость витания для сферической час­тицы
	v = И(рч-рж^чд                                                                    ,. 7> В Ь P*cw "                                                                      l " ' В области 1 < Re < 103 следует использовать формулу Cw=— (l + 0,17Reft665), а для области 10 s Re s 2-105 Ньютон принимал коэффициент Cw = 0,44. Формулу (1.7) можно записать в виде
	(1.8)
	где К = -^Ад /(3CW) — постоянная Риттингера. Согласно мно­гочисленным данным, при обтекании сферы потоком с Re > 60 примем Cw = 0,4, тогда К = 5,72. Чтобы выбрать для расчета скорости витания соответст- 8

	вующую формулу, необходимо знать Re, в которое также входит скорость vB. Поэтому формулы (1.7) и (1.8) примени­мы для вычисления vB методом последовательных приближе­ний. Расчеты производятся следующим образом. Найдя по одной из формул скорость vB и затем Re, следует проверить, лежит ли Re в области применения этой формулы. При несо­впадении результата необходимо использовать другую фор­мулу. В отличие от вязкой в вязкопластической жидкости (ВПЖ) различные сферы могут находиться в равновесии и при ско­рости vB = 0. Состояние шара, предшествующее движению, характеризуется предельным равновесием. В этом случае сила тяжести уравновешивается силой Wu от действия напряжений по всей поверхности объема V. Предположим, что зависи­мость для Wn имеет вид: Wn = jtd42T0. Приравнивая Wn и R, найдем, что при скорости vB = 0 максимальный размер частицы, которая может находиться в равновесии в ВПЖ, определяется формулой d4 =, &t° ■                                                                         (1.9) (Рч - Рж)9 При движении (vB * 0) шара в вязкопластической жидкости полагают, что суммируются сопротивления, обусловленные вязкостными и пластическими свойствами. Поэтому формулу для силы сопротивления при движении жидкости можно за­писать так:
	Wu = nd24x0 + 3nr)d4vB.                                                           (1.10) Приравнивая (1.10) и (1.3), получаем скорость витания час-
	тицы
		V. =■		(1.11)
	При т0 = 0 выражение (1.11) упрощается до случая обте­кания частиц вязкой жидкостью. Силу сопротивления при различных режимах обтекания ВПЖ можно представить также в виде (1.5), где коэффициент сопротивления Cw разли­чен для каждого режима. Для формулы (1.10) Wn = Kd24x0 + Зщёчув = Cwpm ^-^f,                                        (1.12) 9

	откуда
	Рж 2 4	8с0 { 24 Рж^в Re'
	или Cw= — (1 + ^\ш2± (l + -),                                                    (1.13) Re I, 3Ke) Re { 3} где He = ржт0<22 /r\2; S = xod4 /(r\vB). Полагают, что при Re > ReKp коэффициент сопротивления Cw остается постоянным и равным 0,4. Подставляя Cw = 0,4 в формулу (1.13), находим значения ReKp в зависимости от числа Не: ReKp = ЗОН + Vl + He/45J.                                                    (1.14) Для расчета скорости витания при Re s ReKp рекомендует­ся формула (1.11); при Re > ReKp — формула (1.8). При т0 = 0 по формуле (1.14) для вязкой жидкости получаем ReKp = 60.                                                                            (1.15) Формулы (1.8) и (1.11) удобны для расчетов, когда заранее известно условие обтекания, т.е. известно Re. Однако при вычислении скорости витания нельзя сразу определить число Рейнольдса, так как в него также входит неизвестная ско­рость витания. Преобразуя формулу (1.7), которая справедли­ва для вычисления скорости витания в любой жидкости, и подставляя в нее
	f                                                                           (1.16) d4p получаем CwRe2 = -Ar,                                                                       (1.17) где Аг — безразмерный комплекс — число Архимеда, Аг = ^рж(рч-рж).                                                               (1.18) и Подставляя (1.6) в (1.17), находим для вязкой жидкости ю

	Re = Аг/18,                                                                         (1.19) а для вязкопластической жидкости Re = Аг/18 - Не/3.                                                           (1.20) Введем критическое число Архимеда. Если в (1.19) и (1.20) подставить значения ReKp = 60 и ReKp по формуле (1.14), то получим критические значения числа Архимеда: для вязкой жидкости Агкр = 1080;                                                                         (1.21) для вязкопластической жидкости Агкр = 18(ReKp + Не/3).                                                      (1.22) В практических примерах скорость витания следует вы­числять следующим образом: определить Не, ReKp, Агкр и Аг и сравнить Агкр и Аг. Если Аг < Агкр, то скорость витания можно вычислить по формуле (1.16) с использованием (1.20); если же Аг > Агкр, то вместо (1.20) надо использовать формулу (1.17), приняв Cw = = 0,4. При роторном бурении вынос породы осуществляется при вращающейся колонне труб, поэтому частичка шлама имеет не только вертикальную составляющую скорости обтекания, но и горизонтальную. При этом экспериментально установ­лено, что условия выноса шлама улучшаются. При выборе расхода промывочного агента, необходимого для выноса шлама из кольцевого пространства, требуется за­дать скорость потока, превышающую скорость витания, т.е. чтобы скорость частицы v4 была больше нуля. На основании практических данных эту скорость принимают равной 20 — 30 % скорости витания: v4 = (0,2*0,3)vB. При бурении шарошечными долотами пород, способных к хрупкому разрушению, в основном образуются частицы с эквивалентным диаметром менее 10 мм. Поэтому в этих формулах диаметр выносимой частицы d4 = 0,01 м. Частички с меньшим диаметром будут легко выноситься, а с большим диаметром (их всего несколько процентов) — повторно из­мельчаться долотом. Очень часто рассчитывают скорость v4, используя формулу (1.8) и заранее предполагая, что Re > 60. Исходя из специфики опыта бурения в каждом районе, скорость vn выбирают в пределах 0,4 —1,4 м/с. Ближе к ниж­ней границе значения получаются при использовании утяже- п

	ленных глинистых растворов с повышенными реологически­ми свойствами. При применении технической воды и других жидкостей с пониженными реологическими свойствами, осо­бенно при разбуривании глинистых пород для устранения сальникообразования, скорости vn повышают. Расход жидкости в кольцевом пространстве, требуемый для выноса шлама, рассчитывается по формуле О = vnFK, где FK — площадь поперечного сечения кольцевого простран­ства.
	1.2. УСТАНОВИВШЕЕСЯ ТЕЧЕНИЕ ЖИДКОСТЕЙ В ЭЛЕМЕНТАХ ЦИРКУЛЯЦИОННОЙ СИСТЕМЫ СКВАЖИНЫ Рассмотрим расчет давлений при ламинарном течении вязкой несжимаемой жидкости в круговых щелях, трубах и концентричных кольцевых каналах. Течение в круговой щели Задача состоит в получении формулы, связы­вающей перепад давлений Ар = (рс — рк) с расходом Q = = vF, где рс, рк — давление соответственно в отверстии и на контуре щели; v — средняя скорость жидкости через любую цилиндрическую поверхность (рис. 1.2).
	О w(z) т О
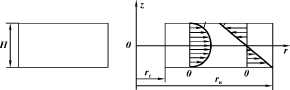
	Рис. 1.2. Эпюры скоростей и напряжений в ламинарном радиальном потоке вязкой жидкости в круговой щели 12

	Для этого требуется совместно решить систему уравнений: движения, сплошности и состояния. Примем следующие граничные условия: w = О при z = ± Н/2; р = рс при г = гс; Р = Рк при г = гк. Реологическое уравнение для вязкой жидкости имеет вид т = ц^.                                                                               (1.23) dz Для такой физической модели известна формула Дарси — Вейсбаха Ар = К^т(г-гс).                                                               (1.24) Art Если г = гк, то Х1 = —/(6); Re = |v|Hp/[x; /(5) = In5/(1 - 6); 6 = гс/гк. При выводе зависимости (1.24) не учитывался в уравнении движения инерционный член w(dw/dr), т.е. рассматривались потери давления, возникающие под действием сил вязкости. При движении жидкости между круговыми пластинами зна­чения Ар, вычисленные только по формуле (1.24), в результа­те неучета инерции могут быть сильно заниженными или за­вышенными относительно общего перепада давления. Перепад давлений за счет инерции не зависит от вида рео­логического закона жидкости и применим для любой несжи­маемой жидкости. Формулу для его определения можно запи­сать в виде формулы Дарси — Вейсбаха
	где к2-----11 + —|- Результирующий перепад давления Ар = Х^(г - гс) = |APl ± Ар2|,                                     (1.25) АН где X = | V ± Х21. 13

	Заметим, что значение К существенно зависит от направ­ления течения, т.е. от знака Q. При поглощении жидкости следует брать знак минус, а при проявлении (притоке) — плюс. Во многих случаях силы трения и инерции примерно оди­наково влияют на перепад давления. Если вязкость повысить до 1 Па-с, то влияние сил трения значительно увеличится, а влияние сил инерции не изменится. При увеличении расстоя­ния между пластинами основную роль будут играть инерци­онные силы, а при увеличении диаметра скважины — силы трения. Течение в трубах и концентрических кольцевых каналах Задача аналогична предыдущей: определить связь между перепадом давления Ар = | р2 — Pi | и расходом Q = vF, где v — средняя скорость жидкости через попереч­ное сечение канала; F = kR2 = nd2 / 4 — площадь сечения потока в трубе; F = n{d2 - d2) / 4 — площадь поперечного се­чения потока в кольцевом пространстве (рис. 1.3). Для нахождения искомой формулы Ар = Ар (О) требуется решить систему уравнений движения, сплошности и состоя­ния при следующих граничных условиях: w = 0 при г = #! = dji; w = 0 при г = R2 = dc/2; р = pt при z = 0; р = р2 при z = L.
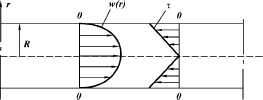
	Рис. 1.3. Эпюры скоростей и напряжений в ламинарном потоке вязкой жидкости в трубе 14

	Реологическое уравнение в этом случае
	дг	(1.26)
	При dH -» О получим расход в трубах (формула Гагена — Пуазейля)
	128ц Можно аналитически получить решение в виде формулы Дарси — Вейсбаха: 2 A           I                  I \ PV Т                                                                                                                 (Л 1П\ Ар = р2 — Р\ \ = К-—L,                                                                      (1.^/1
	где dr = dc — dH — гидравлический диаметр; Х = —/(6) — Re коэффициент гидравлических сопротивлений (5 = d^/dc); W-------(1"5)2 ,;
	In 6 Re = |v|drp/(i. График функции f(5) представлен на рис. 1.4. При dH -» 0 получим dr -» dc, /(6) -» 1, т.е. формулой (1.27) можно пользоваться для вычисления перепада давления в тру-
	1,5 1,4 / (
	Рис. 1.4. График функции /(б)	О 0,2 0,4 0,6 0,8 5 15

	бах, полагая в ней dr = dc. Для удобства расчетов можно за­писать формулу (1.27), раскрывая значения к и Re, в виде: для кольцевого канала
	32n|i		If (6)1=.	-/(5)1;	(1.28)
	Ар	для труб _128HQIL			(1.29)
	Формулы (1.28) и (1.29) справедливы как при течении вдоль оси z(Q > 0), так и против направления оси z(Q < 0). Расчет давлений при ламинарном течении вязкопластических жидкостей в круговых щелях, трубах и концентричных кольцевых каналах Круговая щель Задача состоит в нахождении связи между пе­репадом давления Ар = | рс — рк | и расходом Q = vF, где v — средняя скорость течения через цилиндрическую поверхность F = 2кгН (рис. 1.5) при ламинарном течении ВПЖ (называют также структурным из-за своеобразного распределения ско­ростей, обусловленного наличием ядра течения, движущегося с постоянной скоростью w0). Для нахождения формулы тре­буется решить систему уравнений сплошности и состояния в
	т w(z)=wg w(z)
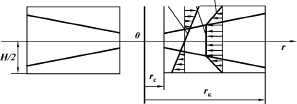
	Рис. 1.5. Эпюры скоростей и напряжений в ламинарном радиальном потоке ВПЖ в круговой щели 16

	11 ■ 0,8 ^--^ ^---------- 06 0,4 0,2 ^» О — ■—-«■
	10'	4 6 810"	4 6 8 10'	4 6 8 S
	Рис. 1.6. График зависимости fS = fS(S) для круговой щели в полулогарифми­ческих координатах области между стенками щели и ядром течения диаметром Но, т.е. при следующих граничных условиях: w = 0 при z = ± Н/2; — = 0 при z = ± Ц/2; dz w = w0 при —Н0/2 s z s Ц/2. Реологическое уравнение для ВПЖ имеет вид т = ±то + т1 —.                                                                       (1.30) dz Для такой формулировки задачи получена формула, позво­ляющая определить перепад давления, предварительно вычис­лив число Сен-Венана S при г = гк и найдя р из рис. 1.6: Ap = |pc-pK| = ^fln^.                                                       (1.31) Щ гс Число Сен-Венана ^ _ лгН2х0
	Можно учесть перепад давлений за счет инерционных сил в общем перепаде давлений, если принять, что последний приближенно равен сумме перепадов Ар = Арт ± Арн, где Арт — потери на трение, вычисляемые по формуле (1.31); Арн — инерционные потери, определяемые по формуле. При Арн знак плюс берется при проявлении и минус при погло­щении. 17

	Течение в трубах В этом случае (рис. 1.7), так же как и в пре­дыдущем, течение имеет ядро радиуса Ro, движущееся со ско­ростью w0. Для нахождения перепада давления пренебрегают членами, учитывающими силы инерции и тяжести, и решают систему уравнений в области между стенкой трубы и ядром при следующих граничных условиях: w = 0 при г = R = dc/2; w = w0 = const при 0 s r s Ro; — = 0 при г = Ro. дг Реологическое уравнение для ВПЖ в трубах при — < О
		дг
	имеет вид dw % = -х0 + г] — при г a Ro. дг	(1.32)
	В результате аналитического решения задачи получают из­вестную формулу Букингама для расхода жидкости, из кото­рой выводят формулу для перепада давления в трубе: Ар = 2то1/(ДР), или, вводя значение диаметра dc = 2R, Ap = ^oL.                                                                                                      (1.33)
	По формуле (1.33) определяют перепад давления Ар (потери на трение) при движении ВПЖ в трубах. Для этого
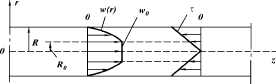
	О                                            О Рис. 1.7. Эпюры скоростей и напряжений в ламинарном потоке ВПЖ в трубе 18

	р 0,8 - 06 «*- 0,4 * 0,2 ft
	6 8 102	4 6 8 S
	Рис. 1.8. Графики зависимости |3 = |3(S) для круговых (i) и кольцевых (2) каналов
	следует вычислить число S, а по его значению определить по кривой 1 (рис. 1.8) величину р и затем по формуле (1.33) най­ти искомый перепад давления Ар:
	s =	(1.34)
	Течение в кольцевом концентричном канале При течениях ВПЖ в концентричном кольце­вом пространстве, так же как и в трубах, образуется ядро, которое имеет форму полого цилиндра с площадью попереч­ного сечения л(Ь2 — а2), боковой поверхностью 2л(а + b)L и движется со скоростью w0 (рис. 1.9). Это ядро разделяет все течение на два градиентных слоя: /, где производная dw/dr <
	о *}('>?•____То
	Рис. 1.9. Эпюры скоростей и напряжений в ламинарном потоке ВПЖ в кольцевом канале 19

	< 0, и II, где производная dw/дт > 0. В связи с этим решают систему уравнений при нахождении профиля скоростей w для каждого слоя отдельно, так как реологическое уравнение имеет свой вид для каждого слоя: для / слоя х = -х0 + ц —;                                                                            (1.35) дг ДЛЯ II СЛОЯ dw                                                                                                       .. ~~. т = то + т1—.                                                                                 (1.36) дг Условие равновесия сил, действующих на ядро, записыва­ется следующим образом: я(Ь2 - а2)Ар = 2ято(а + b)L. Граничные условия при отсутствии скольжения по стенкам кольцевого пространства имеют вид: w = 0 при г = Ri, w = 0 при г = R2. Так как ядро движется с постоянной скоростью w0, то значения распределений скоростей в градиентных слоях на границах с ядром будут w = w0 при a s r s Ъ. Кроме того, должно выполняться условие — = 0 при г = а и г = Ъ. дг Решая систему дифференциальных уравнений для приве­денной модели, получают формулу для определения перепада давления в кольцевом канале: Ар-----^_.                                                                      (137) P(dd)
	Коэффициент р (см. рис. 1.8), предварительно вычислив число S, находят по известному расходу, реологическим т0, г\ и геометрическим dc, dH данным. Графический метод расчета вручную потерь давления при течении ВПЖ в трубах и кольцевых каналах разработан К.Х. Гродде. 20

	Перепад давления в местных сопротивлениях циркуляционной системы Местные гидравлические сопротивления со­здают элементы циркуляционной системы с переменной формой и размерами каналов, в которых изменяются скоро­сти потока, образуются крупные вихри и возвратные тече­ния. Такими элементами являются: ведущая труба, вертлюг, буровой рукав, стояк, замковые соединения, муфты, пере­водники, долота, центраторы, расширители и т.д. Как показывают опыты, перепад давления Ар в этих эле­ментах можно определять независимо от его относительной длины по формуле Ар = ар О2,                                                                          (1.39) где а — коэффициент гидравлических сопротивлений, кото­рый для каждого элемента в первом приближении можно принять постоянным. Наибольшее значение коэффициент а имеет в забойных гидравлических двигателях, гидромонитор­ных долотах и замковых соединениях типа ЗН. Лишь для немногих простейших моделей местных сопротивлений, на­пример внезапного расширения трубы, коэффициент а мож­но определить теоретически. Обычно его находят экспери­ментальным путем. Коэффициент а наземной обвязки циркуляционной сис­темы находится по формуле а = ас + аш + ав + ак,                                                   (1-40) где ас, аш, ав, ак — коэффициенты сопротивлений элементов обвязки, определяемые по данным ВНИИБТ (табл. 1.1). Таблица 1.1
	Элемент Условный Диаметр Обозначение 1 f\ — 5 —4 обвязки размер, мм проходного в формуле а-10 , м сечения, мм (1.40) Стояк 114 — ас 3,4 140 — 1,1 168 0,4 Буровой 76 1,2 рукав 80 0,93 90 0,52 102 0,3 Вертлюг 75 ав 0,9 80 0,7 90 0,44 100 0,3 Ведущая 112 74 «к 1,8 труба 140 85 0,9 (квадрат) 155 100 0,4
	21

	Ввиду переменной геометрии каналов турбобуры можно считать одним из местных сопротивлений и перепад давления в них также вычислять по формуле (1.39) при а--^=-,                                                                            (1.41)
	где Артн — перепад давления в турбобуре при номинальном режиме его работы на жидкости с известной подачей Ота и плотностью (по паспортным данным конкретного турбобура) Рс- Для геометрически подобных сопротивлений, в частности отверстий долот, каналов замковых соединений и муфт оди­наковых типов, при расчетах формулу (1.39) удобнее предста­вить в традиционном виде: Ap-I^f,                                                                  (1-42) где Ц, = 2aF2 — коэффициент сопротивления; F, v — харак­терная площадь сечения канала и средняя скорость в нем со­ответственно. В каналах замковых соединений в качестве характерной величины принимают площадь поперечного сечения канала труб F = jtdB2/4,                                                                                   (1.43) где dB — внутренний диаметр бурильных труб. Опытные данные показывают, что среднее значение | для каналов замков типа ЗН можно принять равным 7,66, а для замков типа ЗШ | = 1,52. Диаметр каналов замков типа ЗУ и приваренных замков мало отличается от внутреннего диаметра бурильных труб, поэтому потери давления в них незначительны и в расчетах обычно не учитываются. Для определения перепада давления от местных сопротив­лений (муфт, замков и т.п.) в кольцевом пространстве также применяется формула (1.39), в которой в качестве характер­ной берется площадь поперечного сечения кольцевого канала между трубами и стенкой скважины F = л(ё2с - d*) / 4,                                                                           (1.44) где dc — диаметр скважины; dH — наружный диаметр труб. При этом коэффициент Ц, вычисляют по формуле 22

	1-2 *p%-l ,                                                       (1.45) U2d )
	где dM — максимальный наружный диаметр муфты или зам­кового соединения. Для расчета суммарных потерь давления от всех замков или муфт данного типоразмера в колонне нужно перепад давления, выраженный формулой (1.39), умножить на число замков или муфт. Для расчета перепада давлений в долоте также пользуются формулой (1.39), в которой в качестве характерной площади берется суммарная площадь поперечного сечения насадок или промывочных отверстий долота; Ц, = 1/ц2 (ц. — опытный ко­эффициент расхода, зависящий от формы отверстия, физи­ческих свойств жидкости и давления, при котором происхо­дит истечение). На основании многочисленных экспериментов установле­но, что коэффициент расхода примерно равен 0,62 для от­верстия в тонкой стенке; 0,82 для цилиндрической насадки; 0,945 для конической сходящейся насадки (с углом конуснос­ти 13°); 0,98 для коноидальной насадки. Ниже приведены ко­эффициенты расхода для характерных форм насадок буро­вых долот, по данным Б.С. Филатова: Цилиндрические сверления с остроугольными кромка­ми........................................................................................................     0,64-0,66 Сверления с коническим входом.............................................     0,8—0,9 У-образная щель.............................................................................     0,7 — 0,75 Насадки с округлым входом и конусностью (гидромо­ниторные).........................................................................................     0,9-0,95 С помощью показателя, подобного коэффициенту ц, можно охарактеризовать полное гидравлическое сопротивле­ние всего долота любого типоразмера. Для этого при экспе­риментальном определении коэффициента ц следует измерять потери давления не в одних лишь насадках, а во всем долоте, т.е. в канале, составленном из насадок и внутренней полости долота. Гидравлический расчет циркуляционной системы при бурении с промывкой несжимаемыми жидкостями Точность гидравлического расчета процесса промывки скважины зависит в первую очередь от достовер­ности исходной информации. 23

	Некоторые исходные данные к расчету могут быть опре­делены приближенно. К таким данным относятся: диаметр необсаженного ствола скважины, реологические свойства промывочной жидкости, шероховатость стенок труб и сква­жины и т.д. Поэтому при расчете следует пользоваться оцен­ками, позволяющими удовлетворить всем технологическим и геологическим условиям бурения. Так, оценкой снизу для ги­дродинамического давления в кольцевом пространстве сква­жины, исходя из условий создания противодавления на про­дуктивные пласты, является гидростатическое давление столба промывочной жидкости. Для оценки сверху распределения давлений, исходя из условия недопущения гидроразрыва (поглощения) пластов, и при определении давления в насосе целесообразно применять расчетные соотношения и исход­ные данные, дающие несколько завышенные значения пере­пада (потерь) давления в различных элементах циркуляцион­ной системы. При определении расхода промывочной жидкости, обес­печивающего очистку забоя и транспорт шлама в кольцевом пространстве, необходимо знать среднюю скорость течения жидкости в затрубном пространстве vK, обеспечивающую вы­нос выбуренной породы из скважины. При промывке пер­вых скважин на площади скорость vK выбирают по расчету. По мере разбуривания площади и накопления опыта значе­ние vK может уточняться с учетом других факторов (тип раз­буриваемых пород, способ бурения, конструкция долот и т.п.). По известному vK определяется расход промывочной жид­кости, необходимый для выноса шлама: Q=*(d'-d«]vK,                                                                        (1.46) 4
	где dc — диаметр скважины, м; dH — минимальный наруж­ный диаметр труб бурильной колонны, м. Полученное значение Q уточняется проверкой условия, обеспечивающего очистку забоя от шлама: Qz^a,                                                           (1.47) 4 где а = 0,35-5-0,5 м/с при роторном способе и электробуре­нии; а = 0,5-5-0,7 м/с при бурении гидравлическими забойны­ми двигателями. При выборе диаметра цилиндровых втулок насоса значе­ние Q подбирают, ориентируясь на вынос шлама, а диаметры 24

	цилиндровых втулок бурового насоса окончательно выбира­ют из справочных таблиц. Суммарную подачу насосов опре­деляют по формуле О = лшОн, где т — коэффициент заполнения; Он — подача насоса при данном диаметре втулок, м3/с; п — число насосов. Коэффициент т выбирается в зависимости от условий всасывания жидкостей. При наличии подпора на всасывание т = 1. Если всасывание осуществляется из емкостей в грун­те, то при промывке водой т = 0,9 и глинистым раствором т = 0,8. При выборе плотности промывочной жидкости, применя­емой при разбуривании заданного интервала, необходимо учитывать следующие два условия: создание противодавления, препятствующего притоку в скважину пластовых флюидов, предотвращение гидроразрыва. Первое условие имеет вид (1.48) где р — плотность промывочной жидкости, кг/м3; рпд — пла­стовое давление, Па; д — ускорение свободного падения, м/с2; 1К — глубина залегания кровли пласта с максимальным градиентом пластового давления, м; kv — коэффициент ре­зерва. Согласно существующим правилам рекомендуются следу­ющие значения kv и Арр: кр = 1,1+1,15; Арр = 1,5 МПа при 1К < 1200 м; кр = 1,05+1,1; Арр = 2,5 МПа при 1200 м <; 1К <; 2500 м; kv = 1,04+1,07; Арр = 3,5 МПа при 1К > 2500 м. Рассчитанную по формуле (1.48) плотность р необходимо проверить на соответствие второму условию, из которого следует, что давление промывочной жидкости в затрубном пространстве против каждого пласта должно быть меньше давления гидроразрыва данного пласта. Второе условие запи­сывается следующим образом: - (1 - ф) Pmffln                                                                       /J Щ
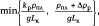	где ф =--------------- — содержание жидкости в шламожидко- 25

	стном потоке без учета относительных скоростей; рг — дав­ление гидроразрыва (поглощения) пласта, Па; 2(Аркп) — по­тери давления при движении промывочной жидкости в за-трубном пространстве на пути от подошвы рассматриваемого пласта до устья скважины, Па; рш — плотность шлама, кг/м3; Ln — глубина залегания подошвы рассматриваемого пласта, м; vM — механическая скорость бурения, м/с. Поскольку значения 2(Аркп) и ф зависят от расхода про­мывочной жидкости, то проверить второе условие можно только после установления подачи насосов. При выборе турбобура расход промывочной жидкости Q, кроме очистки забоя и выноса шлама, должен обеспечить работу турбобура с заданным для разрушения породы мо­ментом Мр. Поэтому необходимо по справочнику подобрать такой тип турбобура, который удовлетворяет следующим ус­ловиям: диаметр корпуса меньше диаметра долота более чем на 10 мм; расход жидкости при номинальном режиме работы Отн близок к принятой подаче насоса; крутящий момент Мт не менее чем на 20 % больше заданного Мр, необходимого для разрушения породы. Крутящий момент турбобура при работе на жидкости плотностью р и подаче насоса Q определяется из соотноше­ния Мт=Мта-Р^-,                                                                     (1.50)
	где Мтн, рс, Ота — соответственно тормозной момент на валу турбобура, плотность и расход жидкости при номинальном режиме его работы. Расчет потерь давления в элементах циркуляционной системы Общие потери давления Ар (в Па) при движе­нии промывочной жидкости в элементах циркуляционной системы определяются из выражения Ар = 2 (Ар,) = 2(Артр) + 2(Лркп) + Лрмт + Лрмк + Лро + + Арт + Ард + Арг,                                                           (1.51) где 2(Артр), 2(Аркп) — потери давления на трение соответст- 26

	венно в трубах и кольцевом пространстве; Армт, Армк — по­тери давления в местных сопротивлениях соответственно в трубах и кольцевом пространстве; Аро — потери давления в наземной обвязке; Арт — перепад давления в турбобуре; Ард — потери давления в долоте; Арг — разность между гидростати­ческими давлениями столбов жидкости в кольцевом прост­ранстве и трубах. Для расчета потерь давления на трение при движении промывочной жидкости без шлама в трубах и кольцевом ка­нале необходимо определить режим течения, в зависимости от которого выбираются те или иные расчетные формулы. Для этого вычисляется значение критического числа Рей-нольдса ReKp течения промывочной жидкости, при котором происходит переход от структурного режима к турбулентно­му. Это число для вязкопластических жидкостей определяется из соотношения ReKp = 2100 + 7,ЗНе058,                                                      (1.52) где He = pd^xo/ti2 — число Хедстрема; г\ — пластическая (дина­мическая) вязкость промывочной жидкости, Па-с; т0 — дина­мическое напряжение сдвига, Па. При течении жидкости внутри бурильной колонны значе­ние dT принимается равным внутреннему диаметру бурильных труб dT. В затрубном пространстве dT определяется как раз­ность между диаметром скважины dc и наружным диаметром бурильных труб dH. Если число Рейнольдса Re движения жидкости в трубах ReT или кольцевом пространстве Re^ больше вычисленного зна­чения ReKp, то режим течения турбулентный. В противном случае движение происходит при структурном режиме. Значения ReT и ReKn определяются по формулам: ReT = pvTdT/ri = 4pQ/jtdTri;                                                 (1.53)
	R         Р^кпК-^н)-------jpO_ i)              ™(dc-dH)i'                                                                  ' где vT = AQ/(ndA, v™ =----------- — средняя скорость жидкос- ти соответственно в трубах и кольцевом канале; ат, ан — соответственно внутренний и наружный диаметры секций бурильной колонны, состоящей из труб одного размера, м. При турбулентном режиме течения потери давления по длине канала определяются по формуле Дарси — Вейсбаха: 27

	внутри труб ^ ^                                                           (1.55) в кольцевом пространстве f™ I,                                                                      (1.56) где 1 — длина секции бурильных труб одинакового диаметра dT или dH, м; Хт, Хкп — коэффициенты гидравлического со­противления трению в трубах и кольцевом пространстве. Их значения следует вычислять по формулам: 0,25
	— + — | , dT KeT) 6к 10° ^	(1.57
		(1.58
	c-ds
	Шероховатость к для стенок трубного и обсаженных уча­стков затрубного пространства принимают равной 3-10~4м, а для необсаженных участков затрубного пространства — 3-10" Зм. Формулы (1.57) и (1.58) получены для турбулентных тече­ний в трубах и кольцевых каналах вязкой жидкости. Будем их использовать и для турбулентных течений неньютонов­ских жидкостей, поскольку для них нет полностью под­твержденных экспериментально аналогичных формул. В слу­чае структурного режима течений формулы для определения потерь давления по длине канала имеют вид:
	(1.60)
	где рт, ркп — коэффициенты, значения которых можно опре­делить по графику (см. рис. 1.8), предварительно вычислив число Сен-Венана для труб ST или кольцевого пространства SKn по формулам:
	5т r\vT 4r\Q с _ T0((ic - dH) _ mo(dc - dH)2(dc + dH) 28

	По формулам (1.56), (1.60) определяются потери давления в кольцевом канале между стенками скважины и турбобуром. При этом значениям dH и 1 в формулах будут соответствовать наружный диаметр корпуса турбобура dT и его длина 1Т. Ме­стные потери давления от замков в кольцевом пространстве определяются из выражения /2    2    \ %1 ^                                                (163)
	где 7Т — средняя длина трубы в данной секции бурильной ко­лонны, м; dM — наружный диаметр замкового соединения, м; 1 — длина секции бурильных труб одинакового размера, м. Для секции бурильной колонны, состоящей из труб, име­ющих внутреннюю высадку, вычисляются потери давления в местных сопротивлениях внутри труб по формуле Ap»-i^f.                                                   (1-64) Потери давления в наземной обвязке находят по формуле = (ас + аш + ав + ак)р02,                                         (1.65)
	где ас, аш, ав, ак — коэффициенты гидравлических сопро­тивлений различных элементов обвязки (см. табл. 1.1). Перепад давления в турбобуре вычисляют исходя из кине­матического подобия по формуле Дрт = Дрта-Р^,                                                                          (1.66)
	где Ар,,,, Ота — справочные данные турбобура при номиналь­ном режиме его работы на жидкости известной плотности рс. Перепад Арг вычисляется по формуле Арг = (1 — <р)(рш— p)gL. При промывке без углубления, когда плотности раствора на входе и выходе скважины сравниваются, Арг равно нулю. Определение потерь давления в долоте. Выбор гидромониторных насадок Резерв давления Ард, который может быть реализован в долоте, определяется как разность между давле­нием Ьрн, развиваемым насосом (или насосами) при выбран­ном диаметре втулок, и суммой перечисленных выше потерь давления в элементах циркуляционной системы Ар = 2(Ар,):
	29

	Дрд = bpH - 2(Др,),                                                            (1.67) где Ъ — коэффициент, равный 0,75 — 0,80 и учитывающий, что рабочее давление нагнетания насосов должно быть, со­гласно правилам ведения буровых работ, меньше паспортно­го на 20-25%. По значению Лрд следует установить возможность исполь­зования гидромониторного эффекта при бурении данного интервала скважины. Для этого необходимо вычислить ско­рость движения жидкости в промывочных отверстиях долота vA по формуле
	р,                                                                  (1.68) где ц — коэффициент расхода, значение которого следует принимать равным 0,95. Если полученное исходя из резерва давления значение vA a 80 м/с, то это означает, что рассмат­риваемый интервал можно бурить с использованием гидро­мониторных долот. Следует иметь в виду, что перепад давления, срабатывае­мый в насадках гидромониторного долота, не должен пре­вышать некоторого предельного значения Аркр, определяемо­го как возможностью запуска турбобура, так и прочностью конструктивных элементов долота. В настоящее время этот предел Аркр = 12-5-13 МПа. Поэтому по формуле (1.68) необ­ходимо подобрать такие значения vA и Ард, чтобы выполня­лись условия vA а 80 м/с; Ард < Аркр.                                                       (1.69) При выполнении условий (1.69) рассчитывается суммарная площадь насадок гидромониторного долота Ф по формуле ф = (Q - Qy)/vA,                                                                (1.70) где О„ = d—- — расход (утечки) промывочной жидкости че- рез уплотнение вала турбобура, м/с; к, п — опытные коэф­фициенты, характеризующие негерметичность уплотнения конкретного турбобура. Найдя Оу, необходимо проверить выполнение условий выноса шлама и очистки забоя. Если разность Q — Оу превышает значения расходов, вычислен­ные по формулам (1.46) и (1.47), то названные условия будут соблюдены. 30

	Рис. 1.10. Зависимость утечек жидкости через пяту-сальник турбобура от перепада давле­ния в долоте	v, м /с
			1 1 1 / / —'
	0,008 0,006 0,004 0,002
	о			2 4 6 8Ард,МПя
	Зависимость Qy от Ард для каждого конкретного турбобу­ра легко найти экспериментально. Приближенное значение Qy можно определить по рис. 1.10 для турбобура 5ТСШ-195ТЛ. По значению Ф подбирают диаметры насадок гидромони­торного долота. Если для данного долота vA < 80 м/с, то следует сделать вывод о том, что бурение данного интервала с использовани­ем гидромониторного эффекта невозможно. В этом случае необходимо вычислить перепад давления в долоте по формуле (1.71)
	1.3. УСТАНОВИВШЕЕСЯ ТЕЧЕНИЕ ГАЗА И ГАЗОШЛАМОВОЙ СМЕСИ В ЭЛЕМЕНТАХ ЦИРКУЛЯЦИОННОЙ СИСТЕМЫ СКВАЖИНЫ При бурении скважины с продувкой газом, при газовом фонтане, при равновесном бурении определение давления в циркуляционной системе скважины и выбор компрессоров становятся необходимой инженерной зада­чей.
	31

	Распределение давлений в восходящем потоке газа и газошламовой смеси в кольцевом канале скважины Движение газошламовой смеси в кольцевом канале скважины имеет место при бурении с продувкой. Это двухфазное течение: первая фаза — шлам, вторая — газ. В этом случае одномерного установившегося двухфазного тече­ния система уравнений примет вид: уравнение движения — = д cos сфшф + р(1 - ф)] ± —с- [pmv^ + pv2(l - ф)] -dz                                           2dT -ршушф^-р(1-ф)у —;                                                   (1.72) dz                   dz уравнения сплошности фFpшvш = Ошрш = тш = const; (1 - y)Fpv = Ор = т = const;                                         (1.73) термодинамическое уравнение р = pRTz,                                                                           (1.74) здесь z — текущая глубина скважины с началом отсчета на устье; p{z) — текущее давление; д — ускорение свободного падения; а — угол между осью z и направлением силы тяже­сти; Ош, Q, рш, р, vm, v — объемный расход, плотность, ско­рость шлама и газа соответственно; ф — объемная концент­рация шлама; dc, dH — наружный и внутренний диаметры кольцевого пространства; F — площадь поперечного сечения кольцевого пространства; R — газовая постоянная; Т — аб­солютная температура; кс — коэффициент гидравлическихсо-противлений; z — коэффициент сверхсжимаемости. При рассмотрении системы (1.72) — (1.74) считают, что z = const, Т = const. Для выбора параметров z и Т можно рекомендовать методику, используемую при исследовании газовых скважин. Для расчета коэффициентов гидравличес­ких сопротивлений в кольцевом канале кс пользуются фор­мулой (1.58), в которой Re определяют для потока газа без учета шлама. Для кольцевого пространства число Рейнольдса Re = vpdT = ц 32

	В дальнейшем, считая ф « 1, вычисляют Re по формуле Re =
	При F, dr, ц, Re постоянных, следовательно, и Хс = const. При рассмотрении движения газошламовой смеси в коль­цевом пространстве пренебрегают инерционными членами и считают, что проскальзывание между шламом и газом отсут­ствует, т.е. vm = v и режим течения — турбулентный. Тогда Ф = Qm/{Q + 0ш), т.е. истинная концентрация ф равна ис­ходной р. Уравнения (1.72), (1.73) и (1.74) в этом случае преобразуют к виду: ^ = gcosa(pJ3 + р(1 - Р)) + Щрту& + Pv2(l - Р));              (1.75) dz                        ч                              ' 2dT v                                          ' fiFpmvm = тш; (1 - P)Fpv = т;                                                (1.76) Р = ОШ/(ОШ + О);                                                                       (1.77) Хс = const.                                                                           (1.78) Из (1.76) и (1.77) следует, что v = vm = (Qm + Q)/F. Под­ставляя выражения для р, v, vm (1.75) и приводя полученное уравнение к безразмерному виду, с учетом (1.74) получают (179)
		d| I + IP где р = р /(zp RТ) — безразмерное давление; Ц, = —?-= — без- RT z размерная координата; г\ = Ошрш/(Ор) = тш/т — массовый коэффициент зашламленности; к2 _ (Ор)2Хс 2(Ррш)2с1Тд' Интегрируя уравнение (1.79), с учетом условия р(0) = р0 получают
	l-KJr] 1 p2 + KJ(l + r|p)2 2Х2г| 2(1 + Я2У -)2 й + ^а+про)2 (i+it2V)2 - arctg(- п - - 2 1 i + it2V р Ри где л2 = л. /cos a.		arctg
			(1.80)
	33

	Из (1.80) при заданном р легко определить Ц,. Нахождение р при заданном | требует решения трансцендентного урав­нения, что сложно, поэтому уравнение (1.79) решают при­ближенно. Заметим, что г\р = Ошршр/(Оршр) = Qm/Q « 1. Пренебрегая в (1.79) г\р по сравнению с единицей, полу­чают ^                  Л£ + %^.                                                 (1.81)
	Решением (1.81) при р(0) = р0 будет Р= |Po+J14exp(2£(l + ri)cosa)--^.                              (1.82) AM          cos al                                      cos a Положив в (1.82) Ti = 0, получают распределение давлений в потоке чистого газа
	P-Jfpo2 + -^-]exp(2|cosa)—^-.                                   (1.83) Ш         cosaj                         cos a В случаях, когда рассматривается движение газа без шлама во всей циркуляционной системе, более естественно вычис­лять безразмерные параметры Kt и р, подставляя в них вмес­то плотности шлама рш плотность газа в нормальных услови­ях.
	Распределение давлений в нисходящем потоке газа в трубах Уравнение для нисходящего потока газа легко получить из (1.79), полагая rj = 0 и принимая во внимание, что член, учитывающий силы трения для нисходящего пото­ка, имеет противоположный знак: -| = pcosa-^.                                                                (1.84) В этом уравнении параметр KY тот же, что и в (1.79), если заменить dT на d, а кс вычислять по формуле (1.57). Если для нисходящего потока давление р0 задано на неко­торой глубине |о, т.е. р(^0) = р0, то решение уравнения (1.84) имеет вид: 34

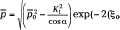		(1.85)
	Из этого уравнения при | = 0, т.е. на устье скважины
	Р= |Ро-^ехр(-2£0соза) + ^^.                                 (1-86) Ш         cosaj                             cosa Статическое давление столба газа получают, полагая в (1.85) £о = 0, Kt = 0. p = p0e?cosa,                                                                           (1.87) или в размерном виде (1.88)
	При движении чистого газа (г\ = 0) в горизонтальной тру­бе (а = я/2) из (1.79) имеем dp /dE, = К? /р. Решением этого уравнения при р(0) = р0 будет
	p = 42Ktl + pz0.                                                                               (1.89)
	Потери давления в насадках долот и замках внутри труб Для вычисления давления р0 над долотом по известному давлению на забое р3 рассмотрим течение газа в насадках долот. Пусть v0, р0, То и v, p, T, р — параметры на входе в долото перед насадкой и на срезе насадки. Будем считать, что при движении газа в насадках основную роль играют инерционные силы. Пренебрегая в уравнении (1.72) силами тяжести и трения и учитывая, что ф = 0, получают i^£ + v*l = 0.                                                                       (1.90) р dz dz Процесс истечения газа из насадок принимают адиабати­ческим: р/р0 = (р/р0)*,                                                                         (1.91) где к — показатель адиабаты (для воздуха к = 1,4). Подстановка (1.91) в (1.90) и последующее интегрирование дают 35

	1 _ ' " ' k-l p0 При v0 « v приближенно из (1.92) получают:				(1.92)
	v-		\Po)		(1.93)
	Из (1.73) следует, что массовый расход газа т = Qp. Тогда массовый расход через одну насадку тп = т/п, где п — чис­ло насадок. Умножив обе части уравнения (1.93) на Фр, где Ф — площадь поперечного сечения насадки, получают
	тп =	= Ф		- l)Po	(1.94)
	Так же, как при получении формулы для несжимаемой жидкости, вводят поправочный коэффициент ц, (коэффи­циент расхода) и окончательно получают
	: " 1)Ро Скорость звука а3 = ^др /др.				(1.95)
					(1.96)
	Звуковое течение — это такое течение, скорость v кото­рого в данном сечении равна скорости звука а3, т.е. v = а3. Приравнивая выражения (1.93) и (1.96), получают
	Ро _(			(1.97)
		U+v
	Из опытов известно, что при режиме истечения р = р3, а при звуковом р > р3. Таким образом, согласно (1.97), звуковой режим будет оп­ределяться неравенством 36

	b.s\-L-\'-\                                                      (1.98) до \к + 1) а дозвуковой режим — (1.99) йэ ' '" ■ " Подставляя в (1.95) значение р из (1.91), р из (1.97) и учи­тывая, что р0 = po/{RToz), получают mn^jzRTog Ро = '
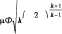	\ТГх) Для дозвукового режима истечения в (1.94) подставляют значение р из (1.73), вместо р подставляют р3, и, учитывая, что р0 = ^Ч, , получают
	(Ц^р                                     (U01) Ро = Рз где I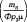тп \2 zRTog(k -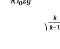
	Формула (1.100) справедлива при условии (1.98), а формула (1.101) — при условии (1.99). Таким образом, по формулам (1.100) и (1.101) можно вычислить давление р0 над входом в долото, если известно давление р3. Для расчетов потерь давления в замках Арзам внутри бу­рильных труб можно пользоваться формулами, справедливы­ми для несжигаемой жидкости: 3,                                                                 (1.102) где dB — внутренний диаметр бурильных труб; п3 — число замков; рс, Qc — средние соответственно плотность и расход газа в бурильных трубах по глубине скважины. Так как рс = Ос = mQc, то 37

	В первом приближении Qc можно вычислить по среднему давлению рс = (рн + рв)/2, где рн и рв — давления в нижней и верхней частях бурильной колонны. Таким образом, Ос = т /рс = mzRTg/pc = 2mzRTg /(pH + рв).                    (1.104) Окончательно
	.                                                                                ( Рн + Рв) Потерями давления от замков в кольцевом пространстве можно пренебречь. Расчет подачи и давления компрессоров при бурении с продувкой Для выбора характеристик компрессора, не­обходимо знать, какой расход газа нужен для очистки коль­цевого канала от шлама и какое давление при этом будет на выкиде компрессора. Для оценки массового расхода газа т найдем отношение скорости витания частицы vB к скорости газа:
	№(рш/р)].                                                         ( 3CW                              m Пренебрегая в (1.106) единицей по сравнению с рш/р и ф по сравнению с единицей, получают (1.107)
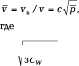	с= ММШ^; р =
	Как видно из (1.107), отношение vB/v = v с ростом давле­ния повышается, поэтому худшие условия выноса шлама из кольцевого канала с постоянным поперечным сечением будут на забое. Для хорошей очистки кольцевого канала от шлама должно выполняться условие v4 a 0,2vB. Условие v — v4 = vB эквивалентно условию 38

	vB /v = c^fp < 1/1,2 = 0,83.                                                (1.108) Если на забое c^jp = 0,83, то в остальных сечениях кана­ла с-^р < 0,83, и условие (1.108) выполнено. На практике площадь поперечного сечения кольцевого ка­нала F часто изменяется с глубиной. Это связано с примене­нием различных по диаметру долот, бурильных и утяжелен­ных бурильных труб и т.п. С изменением F будет изменяться и v, поэтому неравенство (1.108) необходимо проверять в нижних сечениях участков кольцевого пространства с посто­янным F. Если неравенство (1.108) выполняется везде, значит, заданный массовый расход газа достаточен для выноса час­тиц диаметром ёш. В противном случае необходимо найти сечение, в котором v максимально, и увеличивать расход до тех пор, пока не выполнится условие (1.108) в этом сечении. При вычислении v надо пользоваться формулами (1.107) и (1.82). Таким образом, для нахождения необходимого массового расхода следует решить уравнение f(m) = Щт) - 0,83 = 0.                                                        (1.109) Уравнение (1.109) можно решать методом хорд. Для этого выбирают расходы т1 и т2 такими, чтобы выполнялись нера­венства /(mj < 0, f{m2) > 0, и вычисляют т по формуле т = т1-(т*-т1Щщ).                                                            (1.110) f{m2) - /(mj Если при этом f(m) = 0 или немного меньше, то т — ис­комый расход. В противном случае расчет по формуле (1.110) следует повторить. В качестве новых расходов т1 и т2 надо взять расход т и тот из расходов лг,(г = 1, 2), с которым /(лг)/(лг,-) < 0. После определения расхода т последовательно вычисляют давления на забое по формуле (1.82), над долотом по форму­лам (1.100) и (1.101), на устье по формулам (1.85) и (1.86), по­тери давления в замках бурильных труб по формуле (1.103). Суммируя потери давления в замках и давление на устье, по формуле (1.89) определяют давление в конце обвязки, кото­рое равно давлению на выкиде компрессора.

	1.4. УСТАНОВИВШЕЕСЯ ТЕЧЕНИЕ ГАЗОЖИДКОСТНОЙ СМЕСИ В СКВАЖИНЕ Промывка скважин часто осуществляется бу­ровыми растворами, содержащими газ. Цементирование так­же может проводиться газированными тампонажными жид­костями. Газожидкостные среды обладают большой сжимаемостью, обусловленной присутствием в них газа, который может по­ступать в буровой раствор естественным путем, например при разбуривании газоносных пластов, или вводиться в жид­кость искусственно (например, при промывке скважин аэри­рованной жидкостью). Знание распределения давления по глубине скважины при циркуляции газожидкостных смесей позволяет правильно судить о перепаде давлений между скважиной и пластами. Своевременное регулирование пере­пада дает возможность во многих случаях избежать осложне­ний (поглощений, газопроявлений и т.д.). Совместное течение газа и жидкости может происходить при различной структуре потока, определяемой в основном формой и взаимным расположением фаз в потоке. При течении газожидкостных смесей в вертикальных тру­бах и кольцевых каналах условно различают основные четы­ре структуры потоков (рис. 1.11): пузырьковую, характери­зующуюся почти равномерным распределением пузырьков газа в жидкости; пробковую, или снарядную, характеризую­щуюся чередованием в потоке газовых и жидкостных про­бок, при этом размеры газовых пробок становятся соизме­римыми диаметру канала; кольцевую, или пленочную, при которой происходит близкое к разделенному течение газа (в центре канала) и основной массы жидкости в виде пленки на стенках канала; дисперсную, характеризующуюся равномер­ным распределением капелек жидкости в газе. Структура газожидкостного потока прежде всего зависит
	Рис. 1.11. Структуры вертикальных газожидкостных потоков 40

	от физических свойств газа и жидкости, объемного содержа­ния газа и скоростей течения обеих фаз. При подъеме смеси в скважине по мере снижения давления на разных интерва­лах глубины могут существовать различные структуры пото­ка (см. рис. 1.11). В основном в практике бурения встречают­ся две первые структуры потока, при которых поток может двигаться при ламинарном или турбулентном режиме. По­следний наиболее распространен, поскольку наличие относи­тельного перемещения (проскальзывания) фаз из-за их раз­личной плотности (например, в воздуховодяных потоках) способствует перемешиванию, т.е. турбулизации, течения. Относительная скорость между газом и жидкостью снижа­ется в смесях, обладающих неньютоновскими свойствами. В воздуховодяных потоках скорость проскальзывания можно уменьшить до нуля, добавляя структурообразователи: глину, поверхностно-активные вещества и т.п. При этом те­чение воздуховодяной смеси успокаивается и может устано­виться ламинарный режим, который быстрее достигается, если придать воздуховодяной смеси неньютоновские свойст­ва. В частности, в потоке пены перемещение пузырьков газа ограничивается слоями (пленками) жидкости повышенной прочности. Уравнения течения газожидкостных смесей При установившемся ламинарном или турбу­лентном течении и отсутствии фазовых переходов система уравнений при условии, что первая фаза — газ, а вторая — несжимаемая жидкость, примет вид: уравнения движения — = 9 f<PPi + (1 - Ф) Рт\ ± — «PPiVi2 + (1 - ф) р2^! -dz L                                   J м L                                           J ^ + il-ф^Ы                                   (1.111) dz                          dz I (знак плюс берется для восходящего потока и минус — для нисходящего, при этом ось z совпадает с направлением силы тяжести); уравнения сплошности FqppjVj = Qlpl = ml = const;                                             (1.112) F(l — <p)p2v2 = Q2p2 = m2 = const;                                         (1.113) 41

	термодинамических уравнений состояния p = zRTPl;                                                                            (1.114) р2= const,                                                                            (1.115) где z, T — усредненные значения коэффициента сверхсжи­маемости и температуры по глубине скважины; уравнения концентраций ф = ф(р1г р2, vu v2, р, kc) = FJF,                                          (1.116) где F, Fl — площади поперечного сечения канала и его части, занятой газом; уравнения для коэффициента гидравлических сопротивле­ний смеси К = MPi. P2. vlt v2, p, ф).                                                   (1.117) Вводя безразмерные переменные р и |, преобразуют уравнение движения (1.111) к виду
	(Щ                      ' 2 Up
	сЩ                     сЩ	(1.118)
	где К2 = Q2/(gdF2); r\ = Q0p0/Q2p2 = аро/р2 — массовый ко­эффициент аэрации; О0, р0 — объемный расход и плотность газа при нормальных условиях (Го, р0); а = Q0/Q2 — расход­ный коэффициент аэрации. Ламинарное восходящее течение газожидкостных смесей в трубах и кольцевых каналах Рассмотрим ламинарное течение газожидко­стной вязкопластической смеси (например, пены) с равными скоростями фаз. Чтобы получить формулы для расчета дав­лений в трубах и кольцевых каналах, решают систему урав­нений (1.111) - (1.117). Прежде всего определим функции (1.116) и (1.117). Так как фазы движутся с одинаковой скоростью, то 42

	Ф = Р------^l-----------Э-.                                                                         (1.119) Ol+O2 л + Р Поскольку смесь в целом вязкопластическая, коэффициент Хс можно приближенно описать формулой кс = 64/Re',                                                                      (1.120) где Re*------YEiR—;                                                                       (1.121) w'l + ^l I fy-v) v = vl = v2; dr — диаметр трубы или гидравлический диа­метр кольцевого пространства; т0 — динамическое напряже­ние сдвига; \л — пластическая вязкость смеси; р — плотность смеси. Плотность смеси р = PPl + (1 - Р)р2.                                                         (1.122) Как видно из (1.121) и (1.122), число Re* может сильно из­меняться по глубине скважины из-за сжимаемости газовой фазы. Принимают температуру и коэффициент сверхсжимаемос­ти по глубине скважины L постоянными и равными соответ­ственно средним значениям Т, z; динамическое напряжение сдвига т0 и пластическая вязкость г\ также постоянны по глу­бине и равны их средним значениям. Преобразуют (1.121) к виду Re*= v^p .                                                                    (1.123) т4
	Подставляя (1.123) в (1.118), получают 4iJ)(lL ]                                                        (1.124)
	de,           ц + р \р где п = 32цО2 /(dr2Fp2g); m = 16xo/(3drp2g). Разделив переменные и проинтегрировав уравнение (1.124) в пределах от ^ = 0 до Ц, и от р = pY (давление на устье) до р , получают решение в виде £ = P-Pi + At1-B ln^ + В2-АЩ- 2АС х
	43

	x arctg-----^(P-Pi)^-----, д>0,                                       (1.125) Д + (2Ар + В)(2Ар + В)
	где A=l+i) + n + m; B = т](2л + т); С = лт!2; D = Ар2 + Вр = С; Е = Ар2 + Вр1 + С; А = ААС - В2 = 4(1 + л + л + Л1)лт12 - (2л + т)2ц2 = = т]2[4л(1 + л) - т2]-                                                      (1-126) Таким образом, знак А совпадает со знаком выражения в квадратных скобках. Формула (1.125) справедлива для 4л(1 + г\) — т2 > 0 или для ■^^< 91^(1+л),                                                                (1.127) где Re2 = Q2p2dT/{F\i) — число Рейнольдса жидкой фазы. При т0 = 0 всегда справедливо соотношение (1.127), и, сле­довательно, формула (1.125) дает распределение давлений при ламинарном течении вязкой газожидкостной смеси при ф = = р. Соотношение (1.127) характерно для практики бурения, и формула (1.125) позволяет рассчитывать давление по глуби­не скважины. Ее численный анализ показал, что при значе­ниях л ^ 0,2, т < 0,2, л < 0,003 и Ц, а 0,01, встречающихся на практике, последним членом правой части из-за его малости можно пренебречь. В общем случае сжимаемая газожидкостная вязкопластиче-ская смесь может течь при ламинарном режиме на нижнем и при турбулентном на верхнем участках кольцевого канала. Поэтому важно установить, при одном или обоих режимах течет смесь в скважине и на какой глубине происходит смена режима. Так как значения т0, ц заданы для смеси в целом и движение происходит при одинаковой скорости фаз vl = = v2 = v, то для определения режима течения можно восполь­зоваться формулой Re < ReKp - 2100 + 7,ЗНе058.                                            (1.128) Число Re вычисляют по формуле Re = ^-^-= l + a-^g- (1 + л) р_ 2р2г.                                   (1.129) и ^ р)         ч + Р ^ 44

	Скорость v и плотность р найдены с помощью уравнения сплошности при ф = р и уравнений состояния:
	v=			-Р2-
	Подставляя (1.129) в (1.128), найдем значение р*, при кото­ром происходит смена режима. Таким образом, для расчета давлений можно пользоваться формулой (1.125) при значени­ях р > р*, где р* — давление, когда Re = ReKp. При р < р* будет реализован турбулентный режим течения.
	Расчет давления в трубах и кольцевом пространстве для турбулентного течения восходящих вертикальных потоков газожидкостных смесей Е.В. Шеберстовым и Е.Г. Леоновым показано, что при решении уравнения (1.118) для восходящего потока в трубах или затрубье коэффициент Хс можно принять посто­янным и равным 0,05, а функцию истинного газосодержания аппроксимировать для турбулентного течения:
	= 0.81Р при —а 1,93;				(1.130)
	р(	^			(1.131)
	где р = С\ /(С\ + Q2) = Ti /(ti + р) — расходное газосодержание. Тогда, пренебрегая инерционным членом в уравнении (1.118), используя (1.130), (1.131) и интегрируя в пределах от р' до р, получают
	Р-Р					(1.132)
	Р +Роа
	z = ■		пА9		(1.133)
	где
	Ц81
	45

В 1 = 0,19 + ^-2

(1.134)

A2 = n 2

= 2mn; n =

; 2,Ж

г2цп-

jy-

Формула (1.132) справедлива для значений -----а 1,93 или

1-1

Кар0

гг zoro _

(1.135)

1,93 -К а формула (1.133) для р > р*. Для ускорения вычислительного процесса решение уравне­ний (1.132) и (1.133) сведено к соотношению N = М + 1дМ,                                                                 (1.136) где М — некоторая линейная функция от искомого давления р, а N может быть вычислено по известным исходным дан­ным. При N г 5, N s —2 — можно выписать приближенные решения уравнения (1.136): М = N - igN для N г 5; М = 10" аля N <; -2.                                                           (1.137) Если — 2 < N < 5, то решение М можно найти графически на рис. 1.12 из кривых, соответствующих коэффициенту

-М 1,2 0,9 0,6 0,3 О

-  м -    4 -   3 -   2 1,51 -   1

/ 3Ь У, —■ш ^1 1 'J? 3 4 N

б м 0,32 0,24 0,16 0,08

\ — - ^^^^ / -- 1 1, / ^^^^

а=1,0 ОН1'0 Л°>8 о]*0'6

L О

О 0,3 0,6 0,9 1,2 -N 0 0,4 0,8 1,2 1,6-ТГ

Рис. 1.12. Графики для определения чисел М: а - для условий: 1 - 0 < N < 5; 2 - N < 5; 3 - а > 1; Мт < 0; -1,5 < N < 0; б - для случаев: а = 0; а s 1; Моо > 0 (верхнее семейство кривых); а s 1; Мт < 0 (нижнее семейство кривых) 46

	а = 0. После того как М найдено, нетрудно определить дав­ление р. Соответствующие формулы для вычисления N и р: для формулы (1.132)
	аВ,            , аВ,
	s           s S = 2,3ap0 1T Al"Bl; p = MS-p0^-;                                  (1.138) ZOTO At                                       At для формулы (1.133) N = P^i + PL + lg Pi. n5         S\         5
	nA2				p = MSp                                           (1.139)
	При переходе к трубам другого диаметра по глубине скважины (например, УБТ) расчеты следует повторить, при­нимая полученное давление из предыдущего расчета за ис­ходное. Таким образом, можно найти давление на забое р3 при прямой циркуляции или перед долотом при обратной цирку­ляции. Перепад давлений в насадках долот при течении газожидкостной смеси Уравнение движения при vl = v2 = v для рас­сматриваемого случая будет иметь вид
	dp___г. йтг			^ (P)p22^		/^ 140)
		dz
			dz                        dz
	которое можно переписать так: ЁЕ = .РЁХ1,                                                                                        (1.141) dz 2 dz                                                                                                     ' где р = ptp + р2(1 — Р) — плотность смеси; (С\ + О2)/Фс = = v — скорость смеси; Фс — суммарная площадь попереч­ных сечений всех насадок долота. Считают, что газожидкостный поток из насадок полно­стью тормозится, и интегрируют (1.141) в пределах от вычис­ленного давления р3 до искомого рд: 47

	( \2 рд = аро1прд = а£»----------> ----------- + Рз + аро1пр3. (1.142) В уравнение (1.142) введен поправочный множитель \х, — коэффициент расхода, определяемый опытным путем. При расчетах можно принять \х, равным его значениям для одно­фазных жидкостей. Решение уравнения (1.142) также можно свести к виду (1.136), где
	1	д                                             (
	2Фс2ц22,Зар0               2,Зар0 a 2,Зар0 Поэтому для течений в насадках число М находится по тем же правилам, что и для восходящих потоков в кольцевом пространстве. Искомое давление перед долотом рд = 2,ЗМар0.                                                                                    (1.144)
	Перепад давления в турбобурах Движение в турбобуре заменяют течением в трубе и полагают, что движение происходит при равенстве истинного и расходного газосодержания, влияние веса столба смеси и сил инерции незначительно. Тогда уравнение движения примет вид — = —-pv2,                                                                      (1.145) dz ЪХ где \ 2dApTi7                                                                                                                  /1 1 л£*\ Лс =-----——.                                                                                       (1.146) В (1.145) взят знак минус, так как в турбобуре нисходящий поток. В (1.146) d — фиктивный диаметр турбобура; АртОт — перепад давления и расход жидкости в турбобуре при опти­мальном режиме работы на чистой жидкости плотностью р2; F — фиктивная площадь сечения в турбобуре; 1 — длина турбобура. Интегрирование уравнения (1.145) дает формулу 48

	рт = Рь + Agfa + m2)Q2 + аро1пРт+ар°,                        (1.147) Рд + ар
	где Л = ApT/(gp2QT2); m^ + тг = О0р0 + Q2p2; рт - давление на входе в турбобур. Зная Арт, Л, От, по формуле (1.147) можно вычислить не­известное давление рт и таким образом найти перепад давле­ния Ар = рт — рд в турбобуре. Решение (1.147) может быть сведено к уравнению N = М - 1дМ,                                                                     (1.148) где
	2,Зар0
	2,Зар	т2)О2 ^ Рд + ар0 , Рд + ар0 2Зар
	Как видно из (1.149), всегда выполняются неравенства М а а 1/(2,3), N > М. При N s 5 решение можно найти графичес­ки (см. рис. 1.12, а, кривая 2). При N > 5 приближенно М = N + lgJV.                                                                  (1.150) После определения числа М легко найти из (1.149) искомое давление рт = 2,ЗМар0 - ар0 = ар„(2,ЗМ - 1), которое принимается далее за граничное для течения в сле­дующем элементе циркуляционной системы. Расчет давлений в трубах для нисходящего вертикального турбулентного потока газожидкостной смеси Уравнение движения для нисходящего потока имеет тот же вид, что и для восходящего потока, за исклю­чением знака перед членом, характеризующим потери на трение. Пренебрегая инерционными членами, уравнение за­писывают в виде §                  ^(1 О                                    (1.151)
	На основе экспериментальных данных по нисходящему потоку (Е.Г. Леонов, В.И. Исаев)

	Ф- J p, VFr-0,45 где Fr = К2/(I — Р)2 — число Фруда. Подставляя в (1.152) значения чисел Fr и р, получают					(1.152)
	(1.153)
	+р
	где V = г\К/(К - 0,45). Коэффициент гидравлического сопротивления кс для нис­ходящего потока несколько выше, чем для восходящего. Принимают его постоянным и равным 0,06. Используя полученное значение для ф и вводя обозначения
	- + 1
	(1.154)
	уравнение движения записывают в следующей форме:
	Откуда				(1.155)
	Рт-Р , Ч \-i2 2		Г " '
			(1-i)2	(1 - OP -	(1 + г)2
	х Infill		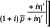		(1.156)
	По формуле (1.156) можно найти давление р в стояке, ес­ли известно давление рт на входе в турбобур. В отличие от восходящего потока, когда правая часть уравнения движения всегда положительна и, следовательно, положителен градиент давления, в нисходящем потоке воз­можен случай отрицательного градиента давления или равен­ства его нулю. Поэтому с ростом глубины скважины давление в нисходящем потоке может как убывать, так и возрастать. Экспериментально это явление отмечено в работе А.О. Межлумова. Чтобы удобнее пользоваться формулой (1.156), вводят обо­значение а = 2гУ(1 + г)                                                                    (1.157) и сводят (1.156) к уравнению 50

	N = М + 0,501g|M - 0,217а | + 0,5(1 - а)2 х xlg|M + 0,217а (1 - а) |,                                               (1.158) где N = Мо + 0,501д|М0 - 0,217а | + 0,5(1 - а)2 х х 1д|М0 + 0,217а (1 - а) | - 1^1 (1 - а)%
	При а = 0 эта формула превращается в (1.136). Последовательность вычисления давлений с помощью формулы (1.158) следующая. По исходным данным (I, dv d2, рт и т.д.) определяются числа г\', Мо, а и знак Моо = Мо — — 0,217а, который совпадает со знаком градиента давления. При а < 1; Моо > 0,5; 5 > N > 0 влияние параметра а не­значительно, и вместо уравнения (1.158) можно воспользо­ваться соотношением (1.136) или кривой 1 (см. рис. 1.12, а). Если N > 5, справедлива формула для М в виде (1.136). Значе­ние М находится на рис. 1.12, б, когда а < 1; Мт > 0; N < 0 или Моо < 0; N < 0. При а > 0; Моо ^0; —2<N<0 значение М можно найти из рис. 1.12, а, а для N < —2 воспользоваться приближенной формулой М = N - 0,51g|N - 0,217а | - 0,5(1 - а)2 х х lg|N + 0,217а (1 - а) |.                                                (1.159) После вычисления числа М находят искомое давление р = M2,3ri'/(l-a),                                                            (1.160) или в размерном виде р = zRTp2gp.                                                                        (1.161) Случай Мо — 0,217а = 0 соответствует значению градиен­та, равному нулю, при этом течение неустойчивое и уравне­ние движения имеет вид: dp / dE, = 0 или р = const. В этом случае при течении нисходящего потока давление по длине участка трубы данного диаметра не меняется. Для расположенных ниже труб другого диаметра расчеты повторяют с начальным давлением, соответствующим конеч­ному давлению, полученному из расчета на предыдущем уча­стке колонны.
	51

	Расчет подачи и давления насосов и компрессоров при бурении с промывкой аэрированной жидкостью Связь между расходом газа О0 при нормальных условиях и подачей насоса Q2 для определенных размеров кольцевого пространства, плотности газа р0, жидкости р2, шлама рч и максимального диаметра d4 выносимых частиц шлама устанавливается формулой
	gd4p4p( 0,108FK2d4p4	-0,008		■	(1.162)
	РоРо
	По уравнению (1.162) можно рассчитывать расходы фаз, обеспечивающие витание шлама в потоке аэрированной жид­кости. На рис. 1.13 (кривые 2—6) построено семейство кривых Q = = f(Q2, p) по точкам, полученным в результате подстановки в уравнение (1.162) фиксированных значений давления р > рр. Здесь рр — заданное давление в скважине против поглощаю­щего горизонта. В дальнейшем рр будем принимать равным пластовому давлению рпд в поглощающем горизонте. Примем также, что кривая 2 (см. рис. 1.13) получена при давлении рр. На рис. 1.14 показана схема системы скважина — погло­щающий пласт. Проектные глубины скважины и поглощаю­щего пласта на схеме обозначены I и 1р, I, — глубина, соот­ветствующая промежуточному положению забоя. Однако для выбора Qo                                                        расходов фаз недоста-
	\ \ \ \ \ у' Л \\ \ 2 у\		точно уравнения (1.162). Из графика (см. рис. 1.13) видно, что вынос частиц шлама из ствола скважины при разбурива-нии поглощающего плас­та, если давление в сква­жине равно пластовому, можно осуществить при
			Рис. 1.13. Графики необходимых расходов газа и жидкости: 1 - обеспечивающие постоян­ное давление против поглоща­ющего пласта; 2-6 - обеспечи­вающие вынос шлама при давлении р,
	Q2-10
	52

	Рис. 1.14. Схема системы скважина - по­глощающий пласт: 1 - долото; 2 - турбобур; 3 - УБТ; 4 - бу­рильная колонна; 5 - поглощающий пласт
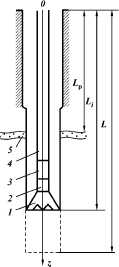	любых соотношениях расходов газа и жидкости, соответствующих различным точкам на кривой 2. Чтобы выбрать конкретные зна­чения О0 и О2 для разбуривания поглощающего пласта, необходимо также учесть давление, создавае­мое потоком аэрированной жид­кости в затрубном пространстве, с помощью уравнений (1.132) и (1.133). Совместное решение уравнений (1.162) и (1.132) или (1.162), (1.132) и (1.133) дает единственное сочетание расходов фаз, обеспечивающих одновременно витание частицы в призабойной зоне и заданное дав­ление на поглощающий пласт. Система уравнений (1.162), (1.132) и (1.133) решается при по­мощи компьютера.
	1.5. НЕУСТАНОВИВШИЕСЯ ТЕЧЕНИЯ НЕСЖИМАЕМОЙ ЖИДКОСТИ ПРИ СПУСКОПОДЪЕМНЫХ ОПЕРАЦИЯХ Спускоподъемные операции (СПО) колонн при различных технологических процессах сооружения скважин часто сопровождаются осложнениями (гидроразрывом вскры­тых скважиной пород, поглощениями промывочной жидкос­ти, обвалами, пластовыми флюидопроявлениями и т.д.). Эти осложнения в ряде случаев возникают из-за недопустимых гидродинамических давлений, вызванных движением колонн в жидкости, заполняющей скважину. Во время СПО колонна обычно перемещается с перемен­ной скоростью ит. Схематично графики скорости и ускоре­ния колонны в зависимости от времени t показаны на рис. 53

	1.15, где участок 0 — it соответствует разгону колонны, учас­ток it —12 — движению колонны с постоянной скоростью, участок t2 — t3 — торможению колонны. Спускоподъемные операции проводят с открытым и за­крытым нижним концом колонны. При этом часто прихо­дится рассчитывать распределение гидродинамического давле­ния в трубном и затрубном пространствах, когда промывоч­ную жидкость можно принимать несжимаемой. Для несжима­емой жидкости р = const;                                                                          (1.163) — = 0.                                                                                 (1.164) dz Для анализа распределения давления в скважине и влияния на его формирование гидравлических характеристик потока жидкости можно записать уравнение в следующем виде:
	_д£_ dw 1 д(п)		(1.165)
	dz         dt г дг Первый член правой части уравнения (1.165) выражает скорость изменения количества движения в единице объема и равен для несжимаемой жидкости произведению плотности на ускорение (инерционная составляющая градиента давле­ния); второй член при стационарных течениях определяет распределение давления и отражает взаимодействие внешних сил и сил трения между слоями жидкости. Граничные и начальные условия для скоростей в трубах и кольцевом пространстве следующие: а
	о	/ — \ t 7 ' 2 * } * t	Рис. 1.15. Качественные графики скорости (а) и ускорения [б] дви­жущейся в скважине бурильной колонны
	б {III! W
	54

	w  =  w(r) при t = 0; w  =  ± uT(i) при r = Rv t > 0;
	tv  =  0 при r = i?2, i a 0;	(1.166)
	w  =  ± uT(i) при г = Ro, t > 0, где w(r) характеризует скорость установившегося течения, вызванного подачей насосов до начала процесса СПО; uT(i) — скорость движения трубы. На рис. 1.16 показаны характерные профили скоростей ламинарного и турбулентного потоков в кольцевом прост-
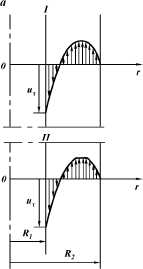		б
		0 X II r 0 «т \ w r III 0 .; Ik R2 r
	Рис. 1.16. Эпюры скоростей в кольцевом канале при спуске (а) и подъеме (б) труб: / - турбулентное движение; II - ламинарное движение; III - движение при >
	55

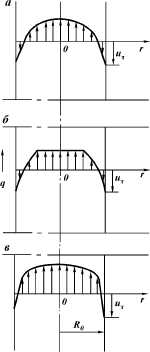		Рис. 1.17. Эпюры скоростей внутри опускаемой в жидкости трубы: а - вязкая жидкость; б - ВПЖ; , -турбулентное движение жидкости
	ранстве, а на рис. 1.17 — возможные профили скоростей внутри движущейся трубы. Согласно (1.164), скорость потока жидкости w = w(r, t) — функция только радиуса и времени. Поэтому можно опреде­лить расход «2 q = q(t) = 2nCw{r, t)rdr,                                                      (1.167) который должен быть равен сумме расходов
	56

	g = gH ± g,,                                                                       (1-168) где gH — подача насосов; qB — расход жидкости, вытесняе­мой нижним концом колонны при спуске или заполняющей пространство под колонной при ее подъеме. Гидродинамические давления при спускоподъемных операциях в скважине, заполненной вязкой жидкостью Рассмотрим движение вязкой жидкости в кольцевом пространстве при спуске колонны с закрытым нижним концом для времени tl s t £. t2 (см. рис. 1.15). Полу­ченные формулы будут справедливы также для расчетов рас­пределения при подъеме колонны. В период i2~*i движение установившееся. Считая, что геометрические размеры колон­ны и скважины неизменны, в (1.165) следует положить dw/dt = 0, тогда ар _ 1 а(лс) dz г дг Решая это уравнение с учетом зависимости для т вязкой жидкости, находят w = —r2 + blnr+C,                                                            (1.169) 4ц где А = ?Е = -±Р;                                                                             (1.170) Bz              L                                                                                                                                          У               ' L — расстояние до рассматриваемого сечения скважины, от­считываемое от поверхности жидкости у устья; ось z направ­лена вверх. Для этого участка граничные условия (1.166) станут следу­ющими: w = 0 при г = R2;                                                             (1-171) w = -ит при г = #!.                                                        (1.172) Определив коэффициенты Ъ и С в (1.169) и (1.170) с помо­щью граничных условий (1.171) и (1.172), получают распреде­ление скоростей течения вязкой жидкости в кольцевом ка­нале
	57

	4ц		(1.173)
			ln-
	Из (1.173) при uT = О вытекает формула Буссинеска для движения вязкой жидкости в кольцевом пространстве под действием перепада давления Ар. При Ар = 0 (т.е. А = 0) получается профиль скоростей при движении бесконечной трубы. Расход жидкости в кольцевом пространстве получают ин­тегрированием профиля скоростей (1.173) в пределах от i?t до
	q=2nfwrdr= — J                4ц
	R2 R2 2 2				(1.174)
	Этот расход соответствует течению с заданными градиен­том давления и скоростью спуска. При дн = 0 q = qB;                                                                               (1.175) gB = яиЛ2.                                                                          (1.176) Подставив в формулу (1.175) выражения (1.174) и (1.176), получают
	= Jt-	Л9 — Л1		-к
	4ц
	^i ~ R2
	Это равенство разрешают относительно Ар: э-±Ь------------Ь------------. п2                      . . 21                             , .2 2                     I Ri I Ri                i Ri I Можно ввести среднюю скорость					(1.177)
	V = -2— =
	1-62
	58

	тогда R\ 62[62-(i-62)in6-il Последнюю формулу можно преобразовать к виду Др = Х^-1,                                                                       (1.178) 2dr                                                                                                                   ' где Х-°±/(6); Re=P^;f(S)------(iz^irf----.             (U79) Re                      |i                252[52-(l-52)ln5-ll vcp = -ф(5)ит; -ф(б) = 6V(1 - б2); 6 = R,/R2. Для встречающихся в бурении значений 0,4 £ 5 £ 1, X можно вычислять по упрощенной формуле У _ 64 0,456 + 0,3 ~ ReT 1-6 Если спускают колонну с открытым концом, то при вы­числении перепада давления также следует учесть движение жидкости внутри труб. Изложенные выше расчеты давлений при СПО одноразмерных колонн можно распространить на случай СПО составных колонн. При разных режимах тече­ния на различных участках составной колонны труб Ар не­обходимо рассчитывать последовательно. Определим инерционную составляющую давления при спуске колонны, описываемую первым членом правой части уравнения (1.165). Усредненное уравнение неустановивше­гося однофазного движения по сечению кольцевого канала ^ = -p^ + ^v2                                                             (1.180) dz ^ at 2dT ф                                                                                               ' Считают, что при неустановившемся движении правая часть не зависит от z, а для левой части можно записать
	()                                                                         (1.181) Интегрируя (1.180), получают формулу для определения давления в кольцевом канале без учета гидростатического давления на заданной глубине р = ±р„ + Артр + ру,                                                      (1.182) 59

	где
	Bv	cp_ dt
			I; Ар	тр	2dr
	ру — давление в кольцевом канале на устье. В формуле (1.182) знак плюс при Ари берется при разгоне колонны, а минус — при торможении.
	Гидродинамические давления, возникающие при спуске колонны, когда скважина заполнена вязкопластической жидкостью Схема рассуждений для определения гидроди­намических давлений подобна изложенной выше. При уста­новившемся течении находят потери давления на трение в кольцевом пространстве. Затем вычисляют среднюю скорость vcp и инерционную составляющую перепада. Общий перепад получают суммированием двух составляющих перепада давле­ний. Чтобы найти перепад давления в кольцевом пространстве при установившемся течении во время спуска колонны, сле­дует решить систему уравнений при следующих граничных условиях: w = —ит при г = Ri, w = 0 при г = R2.                                                             (1.183) Соответствующий задаче профиль скоростей показан на рис. 1.16. Решение этой задачи относительно расхода q мож­но представить в виде (ДА. Голубев):
	д =	(i-в)2		1-6U-		- — x 3
	(1.184)
	(1.185)
	60

	Уравнения (1.184) и (1.185) можно представить в безраз­мерных параметрах
	1-Ь2	(		4 1-6 +б2 3 (1-6)2		Р
	3 1-6					(1.186)
	(1.187)
	где S = Tod.F/frig); и, = итц/{хоёг). При ит = 0 выражения (1.186) и (1.187) преобразуются в формулы Фредриксона — Берда, а при то-»Оиит*О — в решение СМ. Тарга для вязкой жидкости. Для вычисления параметра S следует находить значение
	Я. = <7н + <7в = <7н +					(1.188)
	При спуске с отключенными насосами (дн = 0) уравнение (1.186) упрощается: (1.189)
	Приравняв (1.184) и (1.189), получают выражения
	41-5 + 52		Ц-5--Ы Р—= 0; (1.190)
	(1-6)2
				3 1-1
	= 62/2P(l-5)2(l-62)				16
	(1.191)
	где
	S = xodr/(r!vcp); vcp = uT6V(l - б2); 6 = R./R, Р = 4xoI/(drAp).						(1.192)
	В.З. Дигалев привел к безразмерному виду формулы (1.184) и (1.185) при дн = 0 и в результате численных расчетов по 61

	р 0,9 0,8 0,7 0,6 0,5 0,4 0,3 0,2 0,1 О	,.- .-.0 f ,■ У/ V t / К // ' 1 i 7 1 1 / 2 i ■//// г 1 1 1 i 1 у / 1 1 1 1 f . // 7/ / 3" i i I I /t /// 1 / 1 i j 4 7/ 1 \ ! i J /' 1' \ 1 / / 1 I h I t /■ h i I! Г Г i // 11 J ' / 4 ■ j Ij 1 i / 1 i r T 7 / / /' ~1_ / / у t f ■к =: .—- к -
		-1
	10 Рис. 1.18.		10           10          10           10 График функции р = p (S, 5)	10	10
	ним построил график р = P(6, S), который показан на рис. 1.18. На этом же рисунке приведены кривые 1 и 2 с рис. 1.8 при vcp = Q/F в каналах с неподвижными стенками. Схема расчета потерь давления на трение следующая. По формулам (1.192) определяют 5, vcp и S. Из рис. 1.18 находят р. Перепад давления рассчитывается по формуле л _ 4тп1
	Формулой (1.192) можно пользоваться при расчетах потерь давлений и при подъеме колонн. 62

	1.6. РАСПОЗНАВАНИЕ ГАЗОВОГО ВЫБРОСА И ВЫБОР РЕЖИМОВ ЕГО ЛИКВИДАЦИИ Газ вымывают из скважины циркулирующей промывочной жидкостью, поддерживая на забое давление, равное или несколько большее пластового, чтобы исключить дальнейший приток газа из пласта. При этом максимальные давления на слабый с точки зрения гидроразрыва пласт на глубине Н в незакрепленной части скважины и на обсадную колонну возникают в процессе вымывания забойной пачки газа из кольцевого пространства при выходе ее верхней гра­ницы соответственно слабому пласту и устью скважины (рис. 1.19). Поэтому при поступлении газа в скважину необходимо распознать (предварительно рассчитать) давление рн на сла­бый пласт и давление рш на устье скважины (на штуцере). Если они не превышают накладываемых ограничений по прочности слабого пласта и обсадной колонны, то происхо­дит выброс, в противном случае — фонтан. Вид аварий устанавливают на основе следующих соотно­шений (Е.Г. Леонов и др.): выброс Рн * Рт'                                                                             (1.193) фонтан Р > Р \ (1.194) Рш > Рк- Здесь рн — давление в кольцевом пространстве в момент, когда кровля вымываемой газовой пачки достигнет глубины Н; рг — давление гидроразрыва наиболее слабого пласта, не перекрытого колоннами; рш — давление на штуцере в мо­мент, когда кровля газовой пачки достигает устья; рк — дав­ление разрыва последней обсадной колонны от внутреннего давления у устья. На рис. 1.19 показано распределение давлений в кольцевом пространстве скважины в различные моменты вымывания пачки газа раствором плотностью р3. Прямая 1 характеризует давление в скважине при вскрытии горизонта с пластовым давлением рпд = Рзд1^, превышающим давление столба 63

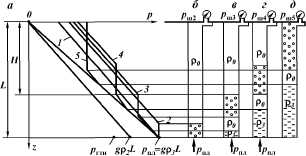
	*Рп
	Рис. 1.19. Графики распределения давления (а) и схемы этапов вымывания пачки газа буровым раствором плотностью р:, (б>-%)>
	раствора плотностью р0, выбранной согласно ожидаемому давлению ргтн, указанному в геолого-техническом наряде; прямые 2, 3, 4, 5 соответствуют распределению давлений в скважине при положениях газовой пачки б, , , „, %о Формулы для опережающих расчетов рн и рш получают, приняв, что на устье скважины работает идеальный регулятор (регулируемый штуцер), обеспечивающий в каждый момент вымывания газовой пачки давление на забое, равное пласто­вому рпд. Вымывать пачку газа можно двумя способами — за­качкой раствора первоначальной плотностью р0 и утяжелен­ного раствора плотностью р3. Согласно упрощенной схеме (рис. 1.20) с раздельным уче­том силы тяжести и потерь на трение, можно записать сле­дующие соотношения:
	- н - iT -
	Др2 = Рн - Рш = РоЭ^ + ~rhH	(1.195)
	или 64

	Рис. 1.20. Схема пере­мещения газовой пачки в затрубном простран­стве скважины: а - начальный момент; б - спустя некоторое время t	а	Ре	б \Рш ш L Ро Ри Ре Ри я о о о о О О О О О О О О о о о о О О О О о о о о о о о о О О О О О О О О о о о о к Ро 1 Ро Ipj- ~_Р-С
	о о о о о о I I I о о
	Рил			|/>ПЛ
	Рт =	-Н-		k2) - p3g(l
	H,                                               (1.196)
	гАек2 = Xv2/(2drg). Очевидно, что РоЛо-Fk = Рн^Л.                                                                   (1-197) где Ло = V/FK; FK — площадь поперечного сечения кольцевого канала; V — объем поступившего на забой газа, рассчитыва­емый по приросту уровня жидкости в приемных емкостях. Во втором уравнении системы (1.196) в члене, учитываю­щем потери давления на трение, примем v = vH. Из (1.197), находя высоту пачки 1Т и подставляя в (1.196), получают квад­ратное уравнение относительно рн, корнем которого, имею­щим физический смысл, является
	Рн = 0,		p	(1.198)
	где Pl = рпд - род(1 + к2) 1Т - р3д(1 - Н - Ц(1 + к2); рПД - 65

	пластовое давление, определяемое в закрытой скважине по формуле рпд = рс + pogL; рс — давление в стояке. По известному давлению рн из (1.196) найдем давление в штуцере рш = Рн - pogw(i + к2).                                                        (1.199)
	При вымывании газа раствором первоначальной плотности Ро(Ро = Рз) давление Pl = рс + родЩ1 + к2) - р0 gLk2.                                   (1.200) При р0 * рз давление pt вычисляется по формуле Pi = [(Рз " Ро)<7 у + Рзд^| • (l + к2) - p3gLk2,                       (1.201) где VT — внутренний объем бурильной колонны, необходи­мый для расчета давления в кольцевом пространстве, создава­емого жидкостью, которая вытесняется из труб. Вид притока также можно установить по приросту объема промывочной жидкости в приемных емкостях. При 0 < V s <; Vnp = FK(p3 - р™,)/ др0 имеет место проявление; при Упр < V <; ^ Кы6 = f— + — + i - 4 " —I — - выброс (р = min[(pr - [РЗ?       Рз                      PsffJ Рпд — родЩ, рк]); при У а Увы6 — фонтан. Плотность утяжеленно­го раствора при этом выбрана так, чтобы уравновесить пла­стовое давление на глубине скважины: Рз = PuJgL.                                                                       (1.202) Точность расчетов рш по формуле (1.199) проверена в про­мышленных условиях. Относительное расхождение между расчетными и экспериментальными кривыми не превышает 20 %. Установив, что обнаруженное поступление флюида на забое соответствует выбросу, можно приступить к расчету режима его ликвидации. Расчет режима ликвидации газового выброса В процессе ликвидации выброса флюид следу­ет вымывать из кольцевого пространства при давлении на забое Рз = Рпл + 8.                                                                        (1-203) 66

	несколько превышающем пластовое рпд. Здесь 5 — заданное превышение забойного давления над пластовым. Если давле­ние на пласт будет меньше пластового, то это приведет к до­полнительному притоку флюида из пласта, что удлинит про­цесс ликвидации выброса, или последний перейдет в фонтан. Если же забойное давление р3 будет значительно выше плас­тового, то могут произойти и гидроразрыв пласта, и погло­щение жидкости, трудно поддающиеся ликвидации. На практике можно судить о забойном давлении по давле­нию в стоке pc = p3-pcpgL + KcQ2^,                                                       (1.204) Ро где Р„-Г-Р-^Г'-Ч                                             (1.205, Pep ~~ усредненная плотность раствора в бурильной колонне; V3 — объем закачанной в бурильную колонну утяжеленной жидкости плотностью р3; VT — внутренний объем бурильной колонны; д — ускорение свободного падения; Кс=(РнО-рш)/О2н;                                                             (1.206) Кс — коэффициент пропорциональности, определяемый до поступления пластового флюида; Он, рн0, р0 — подача насо­сов, давление в стояке и плотность раствора в скважине в момент поступления флюида. Коэффициент Кс получен при предположении равенства соотношений между потерями давления и расходом жидкости в циркуляционной системе при бурении и ликвидации вы­броса. Чтобы в этих случаях отличие в значениях Кс было минимальным, рн0, рш, Он следует измерять в начале отра­ботки каждого долота при открытом устье скважины, когда Рш - Ро- Управлять забойным давлением р3 можно, изменяя пло­щадь проходного сечения штуцера, плотность и подачу на­гнетаемой в бурильную колонну промывочной жидкости. Вы­бор способа ликвидации выброса зависит от параметров и количества промывочной жидкости, имеющейся на буровой в момент выброса, а также от технической характеристики циркуляционной системы. При заданных подаче Q и плотности жидкости р3 забой- 67

	ное давление р3, можно поддерживать равным р3 с помощью регулирования перепада давления в штуцере рш так, чтобы давление в стояке удовлетворяло уравнению (1.204). В этом случае в начале вымывания флюида из скважины, чтобы обеспечить на забое нужное давление р3, в стояке необходи­мо поддерживать давление Рс /v,.o = Kc02 + Рсз + Ь,                                                      (1.207) где рсз — давление в стояке закрытой скважины при опреде­лении пластового давления. Расчет давления на устье при глушении газового фонтана прямой закачкой задавочной жидкости в скважину В условиях возникновения газового фонтана, если устье скважины не разрушено и его прочность доста­точная, закачивают задавочную жидкость. Начав закачку жидкости, закрывают задвижки на выкиде для сброса газа и задавливают скважину. В ряде случаев задавочную жидкость закачивают также через бурильные трубы (чаще через одну трубу), неглубоко спущенные в скважину. В процессе закачки жидкости давление на устье возрастает, стремясь к пластово­му, за вычетом давления столбов жидкости и газа в скважи­не. Приведем расчет изменения давления на устье во времени в процессе глушения при задаваемых расходах задавочной жидкости. Изменение давления на устье в процессе глушения необходимо знать при выборе характеристик и режимов ра­боты насосов и цементировочных агрегатов для глушения, а также для сохранения целостности обсадной колонны и оборудования устья, прочность которых на разрыв иногда бывает ниже избыточного давления газа в закрытой и полно­стью опорожненной от жидкости скважине. Изменение давления на устье во времени можно опреде­лить из совместного рассмотрения движения нисходящего потока задавочной жидкости в скважине и притока газа из пласта. При поршневом нагнетании задавочной жидкости с заданным расходом в любой момент времени iAp(i) = р3 — — ру — перепад давления между давлением р3 на границе раздела газа и жидкости и давлением ру на устье примем в виде разности потерь давления на трение Лрт и гидростатиче­ского давления Арс.

	Тогда = Рз - РУ = ЛРс - ДРт-Потери давления на трение жидкости		(1.208)
	(1.209)
	где V = Q3/F — скорость задавочной жидкости; Q3 — рас­ход задавочной жидкости; Е — площадь поперечного сечения скважины; It — расстояние от устья до границы раздела газа и жидкости в скважине. Гидростатическое давление столба задавочной жидкости рс = p3gLv                                                                                 (1.210) где Ll — глубина Ly = vt.                                                                              (1.211) Здесь t — время от начала глушения. Учитывая (1.209) — (1.211), из (1.208) можно найти давление на устье Ру = ———t-pgvt + p3.                                                         (1.212) Глушение часто осуществляют прямой закачкой (в "лоб") задавочной жидкости в фонтанирующую скважину.
	Ру Рпя
	Рис. 1.21. Графики измене­ния давления на устье в про­цессе глушения скважины при различных расходах (О, < О2 < О3 < О4)
		In/

	Газовые фонтаны глушат прямой закачкой в скважинах с целым устьем, оборудованным закрытыми превенторами, через выкидные линии которых истекает газ. При глушении газ направляют в один или несколько выкидов. Через другие выкиды, обвязанные с цементировочными агрегатами и бу­ровыми насосами, нагнетается буровой раствор. В каждом конкретном случае глушения фонтана, задаваясь значениями расхода 03 и плотностью р3 задавочной жидкос­ти, по формуле (1.212) можно построить зависимость давле­ния на устье от времени задавки. Затем, пользуясь получен­ной графической зависимостью py{t), выбрать практически приемлемый режим закачки задавочной жидкости и оборудо­вание для его осуществления. На рис. 1.21 приведены харак­терные зависимости py{t), построенные по формуле (1.212). Следует отметить, что изложенный метод глушения газо­вых фонтанов прямой закачкой задавочной жидкости наибо­лее эффективен при ликвидации притока газа из пластов, обеспечивающих медленное восстановление давления в сква­жинах после их закрытия. В этих случаях, располагая увели­ченным периодом времени на глушение, в скважине удается создать большой столб задавочной жидкости и тем самым снизить кривую py{t) — кривую прироста давления на устье.