Литература(Разное)

Всё про нефть и газ \Главная \Начало \Литература \Подразделы \Разное \бурение горизонтальных скважин

ГЛАВА 1 Раздел 3

Принципы измерений

Принципы измерений

 

Местонахождение и координатные системы

            В недавнем прошлом, люди должны были описывать свое местоположение тем или иным способом. В настоящее время в нефтегазоиндустрии, как и в остальных об­ластях человеческой деятельности, был осуществлен переход от относительного указа­ния местоположения к абсолютному (т.е. от, например, ”цель находится относительно какой-либо точки на поверхности в направлении  48,6⁰ к северо-востоку на расстоянии 1200фт.” к “цель расположена в UTM 6,234,345.67 м север(N) и 474,628.34 м вос­ток(E)”.  Это было вызвано усложнением вопросов, связанных с точным определением местонахождения объектов. Поэтому, в настоящее время требуется знать гораздо больше о системах координат и способах определения точного местонахождения.

            Земля - сфера. Точнее говоря, в действительности она является неправильным сфероидом. Радиус земли на северном полюсе примерно на 13 миль короче, чем на эк­ваторе. Если бы земля была бы размером с биллиардный шар, то человеческий глаз не смог бы заметить эту разницу; но, при установке границ между странами и границ ме­сторождений, эти 13 миль создают много проблем для геодезистов.

            Карты и схемы, применяемые в направленном бурении - плоские. Отображение линий, лежащих на и под поверхностью сферы на плоскую карту - невозможно без компромиссов и внесения контролируемых ошибок.

            В таких науках как геодезия и картография понадобилось проделать большую работу, чтобы у людей, занимающихся направленным бурением, появился довольно сложный, но, в то же время ясный способ отображения своих координатных данных на картах.

 

Географические координаты (долгота и широта)

            Для идентификации место положения точки на земле, ее поверхность мысленно покрывают сетью линий. Обычно их называют меридианами и параллелями. Для дан­ных северного и южного полюсов, которые приблизительно являются концами оси, от­носительно которой вращается земля и некоторой воображаемой линией, лежащей на середине между полюсами,  параллели широты образуются окружностями, опоясы­вающими земной шар и плоскости которых - параллельны плоскости экватора. Если окружности вычерчиваются на поверхности сферы через равные промежутки, разделяя на 90 частей расстояние между экватором и каждым полюсом, то каждый такой проме­жуток называется градусом широты. Окружности нумеруются от 0 на  Экваторе до 90 на Севере. Каждый градус делится на 60 минут и каждая минута делится на 60 секунд дуги окружности.

            Меридианы долготы образуются серией воображаемых линий, каждая из кото­рых пересекается друг с другом  как на Северном, так и на Южном полюсах. Все они пересекаются с линиями широты под прямыми углами и делят Экватор на 360 равных частей. Это и приводит к разделению долготы на 360 градусов. В свою очередь, каж­дый градус разделяется на 60 минут, а каждая минута - на 60 секунд. В то время как длина градуса широты на сфере везде одинакова, длина градуса долготы меняется в за­висимо сти от широты (см. рис. 3-1). На Экваторе сферы расстояние одного градуса долготы равно расстоянию одного градуса широты, но в других частях они - короче .

            Существование полюсов дают возможность естественного положения Экватора в качестве начальной точки отсчета широты, но для нумерации меридианов долготы не существует такого естественного местоположения, так как все они - одинаковы. Таким образом, необходимо определить один из меридианов как начальный, т. е. - первый. История знает о существовании множества опорных меридианов, которые определя­лись национальными амбициями и влиянием какого - то одного государства на между­народные дела.

            На картах Американских колоний 19 века часто указывался такой меридиан, проходящий через Лондон или Филадельфию. На протяжении 19 столетия границы но­вых штатов описывались меридианами, отсчет которых начинался от меридиана, про­ходящего через Вашингтон, который, в свою очередь, лежал к Западу от Гринвича на 77⁰3’02.3”. Гринвичский меридиан получал все более и более широкое распростра­нение на картах в качестве опорного и в 1884 году конференция по меридианам, прохо­дящая в Вашингтоне, постановила ”меридиан, проходящий через центр измерительного инст­румента Гринвичской обсерватории считать начальным меридианом долготы”, устано­вив, что ”долгота должна отсчитываться от этого меридиана в двух направле­ниях по 180 градусов, причем, восточная долгота должна быть положительной (с плю­сом), а западная - отрицательной (с минусом)”.

 

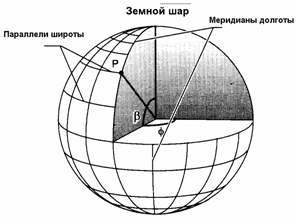
Рисунок 3-1

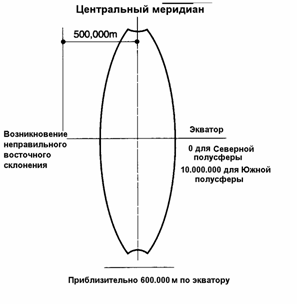
Рисунок 3-2

            При проецировании меридианов на карту, центральный меридиан представляет собой прямую линию и часто принимается за начальную точку или нулевую долготу. Это делается только лишь для облегчения вычислений. После завершения работы над картой, этот меридиан маркируется в соответствии с Гринвичским. В этой главе рас­четы проделаны таким образом, что долгота Гринвича может применяться прямо.

            Понятие долготы и широты ввели греческие и египетские ученые в далекие вре­мена. Большой вклад в развитие этих понятий сделал греческий астроном Гипарх (2 век до н.э.). Клавдий Птолемей в дальнейшем формализовал их. Вследствие того, что лю­бая точка наносится на карту в соответствии со своей долготой и широтой, была разра­ботана прямоугольная сетка для нужд топографистов. Этим способом каждая точка может быть нанесена при помощи определенного рас­стояния от двух взаимно перпен­дикулярных осей на плоской карте.

 

Эллипсоид

            Эллипсоидом называется тело, получаемое вращением эллипса вокруг одной из своих осей. В частности, сжатый сфероид является эллипсоидом, получаемый враще­нием эллипса вокруг своей меньшей оси. Сжатый сфероид - принципиальная форма в моделировании поверхности Земли.

            Земля не является точным эллипсоидом и отклонения от этой формы постоянно развиваются. Для картографирования, однако, эта проблема может быть решена соот­ветствующим подбором констант эллипсоида и незначительные изменения формы Земли в процессе эволюции могут быть учтены при составлении карт различных рай­онов Земли.

            Существует более дюжины принципиальных эллипсоидов, применяемых в од­ной или нескольких странах. Эта разница в размерах получается  не только из-за раз­личной точности геодезических измерений, но и из - за того, что кривизна Земной по­верхности - не однородна из - за неравномерности гравитационного поля. До недавнего времени параметры эллипсоидов подбирались для моделирования формы Земного шара в каком-нибудь конкретном районе страны или отдельного континента.

            Полярная ось модельного эллипсоида для такого конкретного района обычно не совпадала с действительной осью Земли.  Те же самые трудности были и с двумя эква­ториальными плоскостями. Расстояние между их центрами обычно было порядка не­скольких сот метров. Только спутниковую систему измерения координат, такую как, например WGS72, можно считать геоцентрической. Эллипсоиды более поздних моде­лей Земли дают более полное представление о ее форме, чем эллипсоиды с парамет­рами вычисленными на основе измерений на поверхности, но обычно они не являются ”лучшим приближением” для конкретного района.

 

Геодезические параметры

            Геодезические параметры являются определяющими в моделировании поверх­ности Земли. Обычно они состоят из параметров эллипсоида, определяют ориентацию этого эллипсоида относительно земной поверхности, определяют единицу измерения длины, официальное название местности на той поверхности, где они будут приме­няться. Поверхность эллипсоида вместе с ”начальной точкой” отсчета образуют сово­купность геометрических параметров, близко совпадающих с реальной кривизной дан­ной местности и определяют гладкую математическую поверхность, расположенную на среднем уровне моря. ”Начальная точка” определяется широтой, долготой и высотой над поверхностью эллипсоида.

            Выбрав эти параметры, можно выполнять измерения на земной поверхности, будучи ”привязанным” к поверхности воображаемого эллипсоида. Долгота и широта всех контрольных точек в данном районе затем вычисляется в соответствии с поверх­ностью принятого эллипсоида и ”начальной точкой“. В уравнениях, проецирующих этот участок на крупномасштабную карту, необходимо использовать те же самые пара­метры эллипсоида, что и при выполнении геодезических измерений ; в противном слу­чае результат проецирования не будет совпадать с реальной картиной местности. Севе­роамериканская система единиц измерения (NAD27) - наиболее часто применяемая в геодезии на территории США, Канады и Мексики. В Европе наиболее часто применя­ется система (ED50),которая, в частности, используется при разработке месторождений в Северном море. Геодезическая система единиц измерения является частью науки и политики.

 

Проецирование на карту.

            Проецирование на карту - система математических уравнений, устанавливаю­щих взаимно однозначное соответствие между местоположением точек на сферической по­верхности, определяемых параметрами долгота/широта и местоположением точек, ко­торые могут быть нанесены на плоскую карту с некоторыми контролируемыми по­грешностями и известной точностью.

            Наиболее знакомый метод месторасположения является метод прямоугольных координат X, Y. Девяносто девять процентов скважин на поверхности Земли было рас­положено посредством применения этого метода в той или иной форме. Картографиче­ские проекции определяются в специфических величинах длины. Они обычно опреде­ляются коэффициентами, которые меняются в зависимости от месторасположения на поверхности Земли. Для проецирования на карту, геодезические параметры должны выбираться в зависимости от того, какой район отображается.

 

Система UTM

            В большинстве проекций линии долготы и широты - кривые. Квадранты, обра­зованные пересечением этих линий (обычно называемыми параллелями и меридиа­нами) имеют различный размер и форму, что существенно усложняет определение рас­положения точек и измерение по направлениям.

            В системе UTM мир делится на 60 равных зон (каждая шириной в 6⁰) между 84⁰ северной и 80⁰ южной широтами. Для полярных районов применяются другие, специ­альные, проекции. (см.рис.3-2). Каждая зона имеет свое начало при пересечении своего собственного центрального меридиана с экватором  и отображает собой   квадрат. Та­ким образом, на плоской карте, внешние границы зоны - кривые, т.к. они следуют ли­ниям меридиан на круглом глобусе. Каждая такая зона пронумерована, начиная с зоны 1 на 180 меридиане. Площади к востоку и западу от Гринвичского меридиана занимают зоны 30 и 31.

            Любая точка на земле может быть идентифицирована номером своей зоны, рас­стоянием в метрах от экватора (“северное удаление”) и расстоянием от опорной линии Север-Юг (“восточное удаление”). Иногда зоны делятся на секторы, представляющие собой интервалы в 8⁰ широты, начиная с зоны С при 80⁰ С.Ш и кончая зоной Х при 72⁰ Ю.Ш. Буквы I и О - пропускаются. Чтобы определить местонахождение точки на гло­бусе, нет необходимости пользоваться этим методом.

            Чтобы избежать употребления отрицательных величин при обозначении удале­ния к востоку, центральному меридиану каждой зоны, независимо от ее удаления к вос­току, присваивается величина 500,000м. Ширина каждой зоны на экваторе приблизи­тельно равна 600,000 м., сужаясь по мере приближения к полярным областям. В зави­симости от этого, ширина зон меняется в пределах 200,000 - 800,000.

            Для точек, удаленных к северу от экватора, величина смещения на север измеря­ется на прямую в метрах, начиная от 0 на экваторе и возрастая по мере удаления на се­вер. Во избежание отрицательных величин при обозначении удаления от экватора в южном полушарии, экваториальной линии присваивается величина 10,000,000м. и уда­ление на юг в южном полушарии измеряется уменьшающимися, но положительными величинами по мере их удаления.       Фактор шкалы (= расстояние на сетке/истинное рас­стояние) на центральном ме­ридиане равен по определению 0.9996 и  слабо изменяется по мере удаления от цен­трального меридиана.

            Конвергенцией называется разница между направлением на Север по сетке и истинным Севером. Ясно, что на центральном меридиане направление по сетке на се­вер совпадает с истинным направлением. Конвергенция будет слабо изменяться по мере удаления от центрального меридиана и от экватора. Конвергенция - отрицательна для востока и положительна для запада.

            Проектирование скважин обычно осуществляется по координатам сетки карты и, поэтому, направления будут ”привязаны” к ним. Однако, датчики системы телемет­рии, работающие в скважине, ”привязаны ”на истинный или магнитный север. Пользо­ватель обязан, поэтому, уметь преобразовывать эти системы координат из одной в дру­гую.

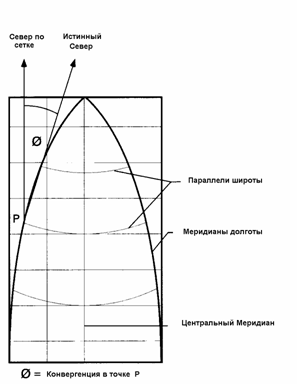
Рисунок 3-3

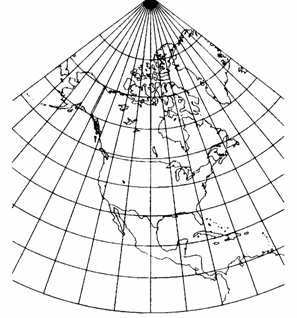
Рисунок 3-4

 

Картографическая проекция Ламберта.

            История.  Именно Ламбертова конформная коническая проекция (рис. 3-4) была первой новой проекцией, представленной Генрихом Иоганном Ламбертом в 1772 г. в той же самой публикации, что и преобразование Меркатора, упомянутое выше. В неко­торых атласах, в частности Английских, это преобразование называют ”конической ор­томорфной” проекцией.

            Основным вкладом Ламберта является нахождение взаимно однозначного ото­бражения плоской фигуры на сферическую поверхность. В этой модели, меридианы - равноудаленные радиусы, а параллели дуги концентрических окружностей. По мере роста широты, расстояние между параллелями увеличивается. Прямые линии между точками апроксимируются на карте дугами больших окружностей.

            Любые две параллели можно принять в качестве стандартных или опорных. В координатной системе США (SPCS) для тех штатов, где применяется проекция Лам­берта, выбор стандартных параллелей - равнозначен эффекту уменьшения масштаба центральной параллели на величину, которую невозможно выразить в простой и точ­ной форме, тогда как в картах, где применяется преобразование Меркатора, просто уменьшается масштаб на определенную величину.

            В США коническая конформная проекция Ламберта принята в качестве офици­альной в тех штатах, которые находятся в самом широком поясе восток-запад. Систему Меркатора применяют для остальных штатов. Одна или несколько зон вовлечены в эту систему в каждом штате. В дополнение, проекция Ламберта применяется на Алеутских островах на Аляске, в Лонг Айленде в Нью-Йорке и северной Каролине, хотя на ос­тальной территории этих штатов применяется проекция Меркатора.

 

Узаконенные координатные системы.

            Термин ”Узаконенная координатная система” используется в данном изложении для официально принятой системы, включающей в себя все вышеприведенные концеп­ции в качестве рабочей при  установке геополитических образований таких как страна, штат, континент и т.п. ”Узаконенная координатная система” установлена законами как на уровне федерального правительства, так и, очень часто, на уровне штатов. Государ­ственная координатная система США  (SPCS) или Национальная система Объединен­ного Королевства являются типичными примерами. В государственной координатной системе США от 1927г (NAD27) приняты геодезические величины, (длина измеряется в футах), и три различные картографические проекции, каждая из которых должна при­меняться в зависимости от расположения точки в конкретном районе США  и эта сис­тема применима ко всем 50 штатам, островам, принадлежащим США и протекторатам.

 

Общие сведения о государственных

геодезических сетях.

Геодезическая сеть состоит из точек, закреплённых на земной поверхности, по­ложение которыхопределено в единой системе координат.

            Геодезическая сеть в нашей стране строится на основе принципа перехода “от общего к частному”. Сначала на территории государства создаётся редкая сеть пунктов, координаты которых известны с большой точностью.

            Затем эта редкая сеть геодезических пунктов сгущается, расстояния между пунк­тами уменьшаются, точность положения пунктов более густой сети понижается.Такой принцип построения геодезической сети России позволяет обеспечить территорию страны пунктами с известными координатами такой густоты, которая необходима для производства инженерных работ и топографических съёмок в дпнном районе.

            При создании геодезической сети на местности производят геодезические изме­рения- измерения горизонтальных и вертикальных улов, расстояний, превышений, при­чём все геодезический измерения производят с контролем их правильно­сти.Результаты геодезических измерений подвергаются математической обработке и позволяют опре­делить плановое или высотное положение пунктов геодезических сетей.

            По своему назначению и точности геодезические сети подразделяются на госу­дарственную геодезическую сеть, сети сгущения и съёмочные сети.

 

Методы создания геодезических сетей.

            Плановое положение пунктов геодезической сети определяется методами триан­гуляции, трилатерации, полигонометрии, а также другими методами.

            Геодезическая сеть, созданная методом триангуляции*, представляет собой сеть треугольников, в вершинах которых расположены геодезические пункты; в этой сети измеряют все горизонтальнае углы и некоторые из сторон - базисы.

            Метод трилатерации** состоит в определении планового положения вершин треугольников, в которых расположены геодезические пункты, измерением длин всех сторон треугольников и одного горизонтального угла.

             В настоящее времяв связи с широким использованием светодальномеров метод трилатерации получает всё более широкое применение.

            Метод полигонометрии*** состоит в построении геодезической сети путём из­мерения расстояний и горизонтальных углов между пунктами. Метод олигонометрии для развития геодезической сети широко применяется в закрытой (залесённой, застро­енной) местности.

 

            Государственная плановая геодезическая сеть.

          Государственная плановая геодезическая сеть служит основой для решения на­учных задач геодезии, для топографических съёмок, для проектирования, строитель­ства и эксплуатации инженерных сооружений.

            Государственная плановая геодезическая подразделяется на четыре класса. Гео­дезическая сеть 1 класса создаёт исходную геодезическую основу для

дальнейшего развития сетей, служит распространению единой системы координат

на всю территорию страны. Сети 2 класса опираются на пункты 1 класса, сгущают её и используются также для решения научно-технических задач. Сети 3 и 4 классов опира­ются на пункты старших по точности классов и используются на пункты старших по точности классов и используются для сгущения этих сетей до необходимой плотности для решения инженерных задач и съёмок. Сеть геодезических пунктов 1 класса состоит

Рисунок 3-5 Схема государственной плановой геодезической сети

из полигонов, образованных звень­ями, длиной до 200 км. и  вытяну­тых вдоль    меридианов   и   парал­лелей ( рис. 3-5 ).   *    - Триангуляция - от латинского слова triangulum - треугольник.   **  - Трилатерация - от латинских слов tri (три) и latus (сторона).     ***- Полигонометрия - от грече­ских слов poln - много,  gwnLa - угол, metrew -измеряю.

 

Государственная координатная система США 1927

(SPCS27)

 

            Государственная координатная система США 1927г. была утверждена в 1930 г. государственным геодезическим комитетом для того, чтобы установить взаимопонима­ние и единую систему для геодезистов, картографов и инженеров (NAD 27). При ее разработке, руководствовались следующими критериями :

*Применение конформных картографических проекций.

*Снижение максимальных масштабных расхождений до уровня менее чем одна часть на 10000.

*Охват всей территории страны минимально возможным числом зон с разными способами проекции.

*Определение границ зон действия  определенных проекций.

            Нельзя нанести на плоскую карту, при картографировании, объекты, находя­щиеся на искривленной поверхности Земли, без нарушения углов, азимутов, расстоя­ний и площадей. Но можно изготовить карту таким образом, что некоторые из этих че­тырех величин останутся неизменными, если выбрать соответствующую ”картографическую проекцию”. Картографическая проекция при которой углы на ис­кривленной земной поверхности, будучи спроецированы на плоскую карту, остаются неизменными – называется ”конформной” проекцией. При разработке государственной координатной системы использовались три конформные проекции. Коническая кон­формная проекция Ламберта, поперечная проекция Меркатора и косая проекция Мер­катора. Проекция Ламберта применялась в тех штатах, форма которых вытянута с вос­тока на запад (напр.  Кентукки, Северная Каролина, Теннеси) или которые предпочи­тали ”разбивку” своей территории на несколько зон, простирающихся с запада на вос­ток. Поперечное проецирование Меркатора использовалось в штатах (или в зонах внутри штатов), простиравшихся с юга на север (напр.  Вермонт, Индиана). Косая про­екция Меркатора применялась в зоне Аляски, где предыдущие методы проецирования не давали удовлетворительных результатов.

Наземные измерения расстояний в 1930г.г. обычно делались при помощи рулетки или чем нибудь еще с еще меньшей точностью. Точность измерений редко превышала 1/10000. Поэтому, разработчики SPCS27 пришли к выводу, что систематические по­грешности масштаба, при проецировании, порядка 1/10000 будут ”поглощены” точно­стью измерений и вычислений. Если измерения расстояний можно будет делать с точ­ностью, превышающей 1/10000, то проблема может быть решена с помощью вычисле­ний, в которых учитывается поправочный коэффициент масштаба. Таким образом, точ­ность 1/10000 была принята в качестве стандартного уровня, но и там, где требовалась более высокая точность, эта система хорошо работала при внесении корректировки.

            При разработке системы SPCS27, для того, чтобы сделать масштабные погреш­ности менее 1/10000, некоторые штаты нужно было разделить на несколько ”зон дейст­вия определенной проекции”. Так, некоторым штатам оказалось достаточной лишь одна зона, некоторым потребовались две или три, а Аляску потребовалось разбить на 10 зон и применять там все три проекции. За исключением Аляски, границы зон опре­делялись границами каждого штата. Обычно существовали значительные области пере­крытия этих зон для возможности геодезических работ на объектах, пересекающих границы зон, где точность должна быть не ниже 1/10000.

            Потребовалось проделать большую работу многим геодезистам и произвести корректировку топографических измерений с учетом поправочного масштабного коэф­-

фициента. С применением этой корректировки, границы зон стали менее важны и лю­бой объект может быть продолжен за границу прилегающей зоны.

 

Государственная координатная система 1983

 (SPCS 83)

            В середине семидесятых годов рассматривалось несколько альтернативных ва­риантов существующей государственной координатной системы. Некоторые геодези­сты защищали старую систему (способы проецирования, границы, определяющие кон­станты), другие полагали, что необходимо принять систему на основе только одной проекции. Сторонники новой системы считали действующую систему слишком гро­моздкой, т.к. она включает в себя три типа проекции и 127 зон.

            Были начаты исследования, цель которых состояла в том, чтобы установить можно ли создать систему, которая бы лучше удовлетворяла принципиальным требова­ниям, чем SPCS 27. Эти требования включают в себя лучшее понимание, упрощение вычислений и применения геодезического измерительного оборудования. В начале ка­залось, что универсальная поперечная система проецирования Меркатора (UTM) - бу­дет лучшим решением, поскольку для нее уже была установлена длина координатной  сетки во всем диапазоне ее использования и основные формулы были идентичны для всех ситуаций. Однако дальнейшие исследования показали, что ее ширина зоны в 6 градусов представляет собой серьезную проблему  для применения геодезистами. На­пример, для того, чтобы расширить зону, необходимо на центральном меридиане уста­новить значение поправочного коэффициента шкалы, равного 1/2500, тогда как на гра­ницах этой зоны, его значение должно быть 1/1250. Как обсуждалось выше, аналогич­ный коэффициент в ”старой” SPCS редко превышал значение 1/10000. В дополнение к этому, корректировочный элемент ”дуга-хорда“, который ”привязывает” наблюдаемый геодезически угол к углам координатной сетки, оказывается завышенным и требует бо­лее частого применения. И наконец, границы геодезических зон не совпадают с гра­ни­цами штатов и других административно- территориальных единиц. Эти проблемы не являлись непреодолимыми, но большинство геодезистов и инженеров считали уже су­ществующую систему SPCS 27 более простой, а UTM не приемлемой из-за слишком резкого изменения фактора масштаба координатной сетки. Исследования снова верну­лись к поперечной проекции Меркатора, но с шириной зоны в 2⁰. Эта координатная сетка удовлетворяла первичным условиям как единая национальная система. Умень­шив ширину зоны, фактор масштаба и корректировка ”дуга-хорда” стали не хуже, чем в сис­теме SPCS 27. Основной недостаток 2 градусной ширины поперечной проекции Мерка­тора состоял в том, что зоны, будучи ограниченными меридианами, редко совпа­дали с границами страны и самостоятельных административных образований.

            Более детальное изучение показало, что, поскольку многим штатам понадоби­лось бы две или более зон, 2⁰ ширина сетки не может быть повсеместно введена из-за несовпадения границ зон с границами административных единиц. Пришлось бы ми­риться с тем обстоятельством, что фактор коррекции масштаба или ”хорда-дуга” в не­которых случаях был бы больше, чем в системе SPCS 27. Кроме этого, среднее число зон, приходящееся на один штат, в этом случае - увеличивается.

            При изучении этой проблемы, стали очевидными три фактора в пользу возврата к идеологии системы SPCS 27.  Эта система была принята в законодательном порядке 37-ю штатами. Существующая координатная сетка применялась на протяжении более 40 лет и большинство геодезистов и инженеров были хорошо с ней знакомы. С появле­нием электронных калькуляторов и компьютеров, появилась возможность уменьшить число зон и типов проекции. Появилась возможность вносить улучшения в систему, не

требующие утверждения в законодательном порядке.  Именно это и послужило причи­ной к возврату к основам философии построения новой системы SPCS 83 по принципу SPCS 27.

Необходимость разработки SPCS 83 вытекала из принятия NAD 83 (Cеверо Американ­ская система данных). В рамках NAD 83  были переопределены новые коор­динаты для всех горизонтальных контрольных точек в Национальной Системе Геоде­зических Опорных Точек (NGRS). Величины NAD 27 больше не отвечали требованиям горизон­тального контроля, необходимого для геодезистов и инженеров и их нужно было пере­считывать в каждом районе для привязки к координатной сетке. Преимуще­ства NAD 83 состояли в следующем :

            *Сто пятьдесят лет непрерывных геодезических наблюдений  (всего 1,8 мил­лиона измерений) постоянно корректировались с математическими расчетами, необхо­димыми для  их  обобщения, устраняя появляющиеся ошибки.

            *Точность межконтинентальной спутниковой триангуляции, точность определе­ния опорных расстояний методами на основе Доплеровского эффекта, интерферомет­рическими методами улучшило точность координатной сетки.

            *Новая форма Земли, согласно Геодезической Системе Отсчета от 1980 г. (GRS 80), которая лучше отражает реальность, чем сфероид Кларка 1866г., который приме­нялся в NAD 27.

            *Начало координат, которое переместили со станции Мидз Ранч, Канзас, в центр массы Земли для лучшей совместимости со спутниковыми системами.

Это не только привело к изменениям геодезических координат каждой контрольной точки, но и потребовало изменить Государственную координатную систему по сле­дующим причинам :

            *Плоские координаты математически вычисляются (при помощи ”картографических уравнений”) из геодезических координат.

            *Новая форма Земли, в соответствии с эллипсоидом GRS 80, определяется от­личными от старой модели параметрами (большая и малая оси, эксцентриситет). Эти новые параметры эллипсоида включаются в картографические уравнения и их исполь­зование дает разницу в плоских картографических координатах.

            *Картографические уравнения стали точными до миллиметра, тогда как старая система, основанная на вычислениях с помощью логарифмической линейки, обычно давала приблизительные результаты.

            *Определяющие константы нескольких зон были исправлены.

            *Численные величины сетки координат каждой зоны были существенно изме­нены, что создавало впечатление существенного отличия координат.

            *Все координаты в Государственной координатной системе были выражены в метрических единицах.

            *В SPCS 83 применялась поперечная проекция Меркатора в приближении Га­усса-Крюгера, тогда как в SPCS 27 применялась форма уравнений Гаусса- Шрайбера.

 

Локальные координатные системы.

            В большинстве случаев, в направленном бурении применяется локальная сис­тема координат в повседневной работе. Эта локальная система имеет прямую зависи­мость от всего того, что обсуждалось выше в этой главе. При определении локальной координатной системы делается много не очевидных, но важных предположений. Не­обходимо тщательно определить локальную координатную систему так, чтобы прямые и подразумеваемые связи с ”законной” системой были сохранены.

            Локальная координатная система должна иметь свое начало в точке, которая должна быть определена в ”законной” координатной системе. Эта точка должна слу­жить в качестве Структурной точки отсчета в случае только одного элемента (плат­форма/буровая) или Опорной точки поля (района), если локальная координатная сис­тема применяется ко всему месторождению. Термин ”Опорная Точка” в этой главе применяется  к любому из этих двух случаев. Опорная точка определена в ”законной” системе координат и в новой локальной системе координат расположена в (0,0). Эта опорная точка имеет только координаты Север и Восток. В дополнение к этому, необ­ходимо определить опорную величину по вертикали для определения правильной глу­бины по вертикали (TVD) и глубины по стволу скважины (MD). При необходимости, можно определить опорную величину вертикали как для MD, так и для TVD.

            Если специально не обговорено обратное, оси Локальной координатной системы сориентированы параллельно осям ”законной” системы координат в которой опреде­лена опорная точка.

            Очевидно, должна быть определена и единица длины. Это обычно диктуется пожеланиями заказчика или правительственными постановлениями.

            По определению, координатная сетка Локальной координатной системы должна использовать Север координатной сетки ”законной системы” для того, чтобы ее можно было правильно нанести. Только в этом случае углы и расстояния могут быть измерены правильно. Если при нанесении данных замеров использовать Истинный Север или Магнитный Север, то взаимосвязь между точками и линиями не будет линейной и по­этому они не могут быть измерены непосредственно рулеткой и компасом.   Очень часто эта ошибка (отклонение) - мала, но иногда она бывает достаточно значительна. Во многих случаях правительственные постановления диктуют необходимость исполь­зовать Север сетки.

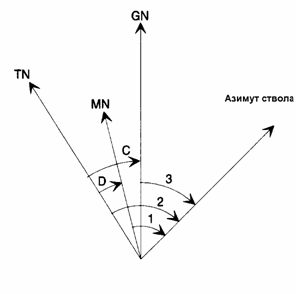Рисунок3-6

Часто бывает нужным преобразовать координаты местоположения точки из од­ной  ”локальной системы” в другую. Хо­рошим примером может служить проект не­скольких скважин, пробуренных с од­ной платформы. В этом случае одной ”локальной” системой координат может служить сама платформа, которая, в свою очередь, распо­ложена в некоторой ”законной локальной” системе, в которой определено ее месторасположение.            Поправкой магнитного наклоне­ния (склонения) является угол между магнит­ным Севером и истинным Севе­ром. Вели­чины магнитного наклонения меняются в зависимости от времени и местоположеия.

Проектировщик мо­жет по своему усмотрению планировать скважины либо в системе платформы, либо в ”законной локальной системе”. Переход из одной системы координат в другую осуществляется параллельным переносом в направлении Север, Восток (+,-) и поворотом осей вокруг начала координат.Если движение магнитного Се­вера - постоянно и предсказуемо, то магнитное наклонение может быть вы­числено в любой данной точке и в любое данное время.

В настоящее время широко используются диаграммы магнитных наклонений и скоро­стей их изменения (обычно выраженные как ежегодно меняющиеся). Склонение в

восточном направлении выражается положитель­ными величинами, а в западном направлении - отрицательными. Несмотря на то, что переход от одной системы отсчета к другой кажется легкой задачей, необходимо быть очень внимательным, чтобы учесть относительные направления конвергенции и маг­нитного склонения. Например, см. рис. 3-6.

Лицензионные границы.

            Лицензионные линии обычно устанавливаются должностными лицами прави­тельственной администрации или агентствами и должны иметь четко определенные границы.

TN=  Истинный Север

MN= Магнитный Север

GN= Север сетки

C=    Схождение (конвергенция) сетки

D=    Поправка магнитного склонения

1=     Магнитный азимут

2=     Истинный азимут= Магнитный азимут + магнитное склонение

3=    Азимут по сетке = истинный азимут- схождение сетки.

Все азимуты и поправки - положительны в направлении по часовой стрелке. 

Любая точка внутри лицензионной площади должна быть определена как расстояние от двух близлежащих линий границы. (См. рис. 3-6).

Однако, это не всегда верно для лицензий на право пользования, которые определялись старыми методами (“граничными метками”). В этом методе направления и расстояния определялись от линий неправильного многоугольника, который охватывал зону поль­зования. Если скважина располагалась в соответствии с этим методом, ее местополо­жение определялось следующими параметрами, см. рис. 3-7.

            * 300.6’ от S43.8⁰ W линии.

            * 248.8’ от N50.2⁰W  линии

В этом случае отсутствуют опорные величины, определяемые национальными или ме­ждународными геодезическими  системами. Этот метод применялся для большинства скважин, пробуренных в Техасе.

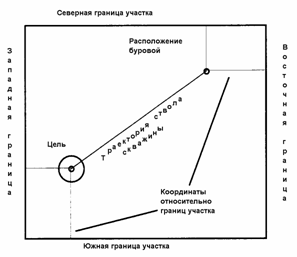
Рисунок 3-7

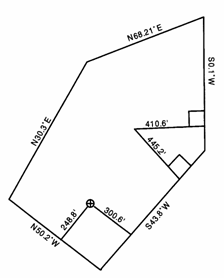
Рисунок 3-8

Скважины, располагаемые на земле.

            Планирование направленных скважин предполагает наличие некоторых ограни­чивающих факторов на их месторасположение. Расположение на земле определяется факторами возможности отклонение ствола от вертикали.

 

Расположение на море

            Основной разницей между буровой, расположенной на поверхности Земли и в море является число и близость стволов скважин. На морских платформах стремятся пробурить от 6 до 60 стволов. Расстояние между их центрами может быть только 6 фу­тов.

            На выбор месторасположения может влиять глубина, толщина слоя песка, ко­ралловые рифы, локальные течения и т.п.

Конечная цель

Геологические условия

            Первый шаг в планировании любой скважины состоит в определении целей. На­правленная скважина может иметь одну или более целей. Это могут быть определен­ные пласты или геологические особенности такие как разломы, выклинивания; другие стволы скважин или их комбинация. Здесь мы рассматриваем способ определения этих целей.

            Как мы уже видели, существует много опорных систем месторасположения на поверхности. То же самое относится и к подземной цели с добавлением вертикальной глубины. При планировании скважины, проще всего использовать локальную систему координат для ”привязки” цели. Если точное положение опорной точки и цели из­вестно, то локальные координаты можно легко определить.

Прямоугольные координаты

            Прямоугольные координаты цели обычно задаются в футах/метрах Север/Юг и Восток/Запад от локальной опорной точки. Они могут быть легко выведены вычита­нием поверхностных координат сетки из координат цели. Например таблица №3-1. По­ложительные величины означают удаление на Север или Восток. Отрицательные вели­чины означают удаление на Юг или Запад.

Полярные координаты можно вывести из прямоугольных координат. Они выражаются как расстояние (удаление) и направление (или квадрант, или азимут). По­лярные координаты получаются из прямоугольных следующим образом :

Азимут = Tg^-1 [(E/Wкоордината)/(N/Sкоордината)]

В вышеприведенном примере : Азимут = Tg^-1 (200/500)= 21.8⁰

            Как мы знаем, цель находится в направлении на Восток и Юг от опорной точки на поверхности. Цель удалена от этой точки в направлении, определяемом углом S21.8⁰ Е или 158.2⁰. Расстояние (удаление) определяется формулой :

Расстояние = [ (E/Wкоордин.)² + (N/Sкоордин.)² ]^1/2

            В вышеприведенном примере : расстояние = (200² + 500²)^1/2 = 538.5

            Таким образом, мы можем считать, что цель удалена на расстоянии 538.5 метров при азимуте 158.2⁰.

            Помните, что эти уравнения не работают при координатах N/S = 0. Знак азимута зави­сит от координаты E/W. Всегда располагайте азимут в правильном квадранте, чтобы функция тангенса была определена на промежутке 0-90⁰. 

	N/S	E/W
Координаты сетки цели Координаты опорной точки Парциальные координаты	6,354,500.00N 6,355,000.00 N - 500.00	262,744.00E 262,544.00E 200.00

 

Таблица 3-1

Полярная Система Координат

            Полярные  координаты  являются  системой,  наиболее  часто  применяемой  при  картировании, поскольку они дают кратчайший маршрут между  двумя точками;  маг­нитный север служит в качестве известной точки; и поскольку сравнительно легко  по­лучить точное направление с помощью магнитного компаса.

            Такой принцип применяется и для измерения в скважинах, за исключением того, что для  однозначного указания конкретной точки в пространстве должен учитываться третий  размер – действительная глубина по вертикали.

            Для определения полярных координат в скважине замеряются значения  глу­бины, угла наклона и  азимута (направления), и используются для определения место­положения точки  посредством тригонометрических вычислений.

 

Азимуты

            Ствол скважины является круглым отверстием, которое не может быть надле­жащим  образом представлено одной прямой линией. Если ее представить в виде ци­линдра, то  для индикации направления скважины может применяться лишь одна линия вдоль длины  ствола скважины. По соглашению, эта линия представляет высокую сто­рону (Н.5.)  ствола.

            При использовании отклоняющего инструмента, например, кривого перевод­ника, для  определения правильно ли сориентирован инструмент, должно быть из­вестно положение “0” кривого переводника. Положение “0” кривого переводника мо­жет считаться измерением,  указывающим, куда пойдет скважина, тогда как ранее упо­мянутое измерение высокой  стороны есть не что иное, как азимут ствола скважины.

            При использовании кривого  переводника/или отклонителя, переводник(и)  бу­дут иметь маркировочную метку, вытравленную или вырезанную на вершине  изгиба. Ориентация маркировочной метки - это угловое положение кривого переводника (или корпуса) относительно ствола скважины.

            Измерительный инструмент (телесистема и т.д.)  не может быть непосредст­венно связан с маркировочной меткой изогнутого элемента. Поскольку измерительные инструменты привинчиваются к кривому  переводнику, и поскольку резьбовое соеди­нение редко собирается так, чтобы совпали  маркировочные метки на двух инструмен­тах, на измерительном инструменте должна  быть собственная маркировочная метка. Хотя возможно собрать забойную компоновку  (ВНА) так, чтобы маркировочные метки измерительного прибора и кривого  переводника в точности совпадали, на практике это встречается очень редко.

 

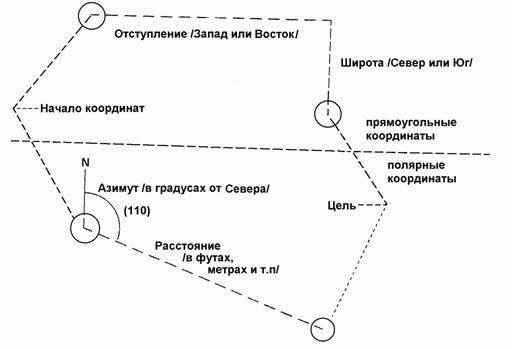
Рисунок 3-9

 

 

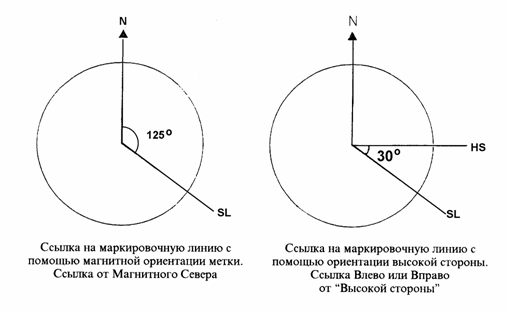
Рисунок 3-10

 

На рис.3-10 приведено возможное соотношение между маркировочными метками кри­вого  переводника и измерительного прибора. Очевидно, что этот угол должен быть измерен  до того, как узел спускается в скважину. Согласно правилам, это измерение  выполняется так, как в случае, если смотреть вниз на верхнюю часть инструмента.

 

Высокая сторона

            Как объяснялось ранее, для определения направления нужна контрольная точка. Это же  справедливо для ориентации маркировочной метки. Можно измерить угол ме­жду  магнитным севером и маркировочной меткой измерительного прибора  или угол между  маркировочной меткой измерительного прибора и высокой стороной ствола скважины;  применяемая контрольная точка зависит от стабильности направления ствола скважины.

 

 

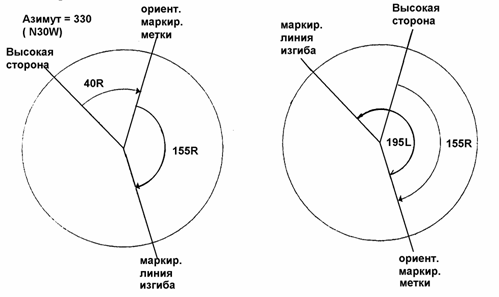
Рисунок 3-11

В истинно – вертикальном стволе скважины нет направления ствола (и нет вы­сокой  стороны). Необходимо связывать ориентацию маркировочной метки (ориента­цию  кривого переводника и, следовательно, долота) с магнитным севером. Теоретиче­ски,  ствол с углом наклона имеет высокую сторону; однако, в промысловых условиях  вибрации и колебания часто трудно установить расположение высокой стороны с  по­мощью акселерометров маятникового типа (при низком угле наклона). Применение  кривого переводника может внести еще большую путаницу. До тех пор, пока  направ­ление ствола не станет достаточно стабильным для того, чтобы обеспечить  надежную контрольную точку, должна применяться магнитная ориентация  маркировочной метки. При достижении скважиной определенного зенитного угла,  направление  стабилизиру­-

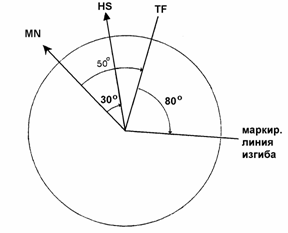
Рисунок 3-12           Рисунок 3-13.

ется, легче связать требуемые коррекции направления с высокой стороной ствола сква­жины: градусы влево или вправо от высокой сто­роны. В стволах меньшего  диаметра или при более твердых пластах это может быть возможно при очень низких  углах на­клона, например, 3 градуса.       В скважинах большого диаметра, с мягкой  литологией или выше забойного двигателя, ствол может оказаться  не за­меренным; поэтому, пока угол наклона сква­жины находится в  пределах 8-10 гра­дусов, довольно часто встречается ссылка на ори­ентацию  маркировочной метки от­носительно "высокой стороны" ствола скважины.         Магнитная  ориентация маркировоч­ной  метки  или  ориентация относительно  “высокой  стороны” ствола скважины  ука­зываются различными путями. При ис­поль­зовании ориентации маркировочной метки относительно  “высокой стороны”, она обычно указывается в виде влево или вправо от “высокой стороны”,  с максиму­мом в любом направлении 180 градусов.       При применении магнитной ориента­ции маркировочной метки, она связыва­ется с  градусами от магнитного севера и термины "вправо" или "влево" никогда не  исполь­зуются (магнитные азимуты всегда вправо (по часовой стрелке) от магнитного  по­люса).

 После сборки КНБК маркировочные метки кривого переводника и измеритель­ного прибора обычно не совпадают. Поэтому при ориентации необходимо учитывать эту раз­ницу.

Всё про нефть и газ \Главная \Начало \Литература \Подразделы \Разное \бурение горизонтальных скважин